美丽而脆弱的天体运动：当C#遇见宇宙混沌

你是否曾仰望星空，惊叹于宇宙那宏大而精准的秩序？行星亿万年如一日地围绕恒星旋转，仿佛背后有一只无形的手在精确地指挥。然而，在这看似和谐的宇宙乐章之下，其实涌动着混沌的暗流。今天，我想通过我最新的一个开源项目，带大家一窥这美丽而又脆弱的天体之舞。

这个项目就是 n-body，一个我用 C# 结合 ode45 高精度常微分方程求解器和 Direct2D 图形渲染，专门用来模拟二维天体运动的“宇宙沙盘”。

从我们熟悉的家园开始

让我们先从最经典的场景开始：太阳-地球-月球系统。这是一个我们从小就熟知的稳定模型。

下面是它的初始参数定义：

public static SystemDef CreateSolarEarthMoon1() => new([

    new(0.3534,  0, 0, -0.2658, BodyType.Solar, 1.0),

    new(-1.1466, 0, 0, 0.8183 , BodyType.Planet, 0.3),

    new(-0.9466, 0, 0, 2.0430 , BodyType.Moon, 0.01)

]);

运行起来的效果，正如你我所预料的那样和谐而稳定：

可以清楚地看到，地球围绕着太阳公转，月球则围绕着地球旋转。但如果你再仔细观察，会发现一个有趣的细节：地球的轨道并非一个完美的椭圆，它在月球引力的作用下，会产生轻微的、周期性的摆动。这正是万有引力定律在微小尺度上展现的魅力。

蝴蝶效应：失之毫厘，谬以千里

天体运动的迷人之处在于其对初始条件的极端敏感性。如果我们将初始参数做一些看似微不足道的调整，宇宙的剧本可能就会完全不同。

比如，我们微调参数，将太阳的质量和位置稍作改变：

public static SystemDef CreateSolarEarthMoon2() => new([

    new(-0.2013, 0, 0, 0.16041, BodyType.Solar, 2.0),

    new(1.2987, 0, 0, -1.0744, BodyType.Planet, 0.3),

    new(1.4987, 0, 0, 0.1503, BodyType.Moon, 0.01)

]);

再来看模拟结果，整个系统的动态就变得狂野起来：

月球被地球和太阳的引力反复拉扯，上演了一出惊险的“太空芭蕾”，最终才勉强稳定下来。这正是混沌理论中“蝴蝶效应”的直观体现：初始状态的微小差异，足以导致最终结果的天壤之别。

完美环状三星：脆弱的平衡艺术

除了我们熟悉的这种主星-行星-卫星模型，宇宙中还存在着更令人着迷的结构，比如刘慈欣《三体》中提到的，也是困扰了无数物理学家和数学家的“三体问题”。

我的模拟器提供了一个可以生成任意数量星体、并让它们进行稳定环状运动的函数：

public static SystemDef CreateStableRing(int N, double scale = 1.0, double G = 1.0, double M = 1.0, double R = 1.0)

{

    if (N < 2)

    {

        throw new ArgumentException("星体数量 N 必须大于等于 2", nameof(N));

    }

    double forceSumFactor = 0;

    for (int k = 1; k < N; ++k)

    {

        forceSumFactor += 1.0 / Math.Sin(Math.PI * k / N);

    }

    double v_squared = (G * M / (4.0 * R)) * forceSumFactor;

    double v = Math.Sqrt(v_squared) * scale;

    BodyDef[] stars = new BodyDef[N];

    for (int i = 0; i < N; ++i)

    {

        double angle = 2.0 * Math.PI * i / N;

        double px = R * Math.Sin(angle);

        double py = R * -Math.Cos(angle);

        double vx = v * Math.Cos(angle);

        double vy = v * Math.Sin(angle);

        stars[i] = new BodyDef(new BodyState(px, py, vx, vy), BodyType.Solar, M);

    }

    return new SystemDef(stars, G);

}

利用这个函数，我们可以创造一个理论上完美而稳定的环状三体系统。它们的轨迹如同精密的时钟，优雅而迷人：

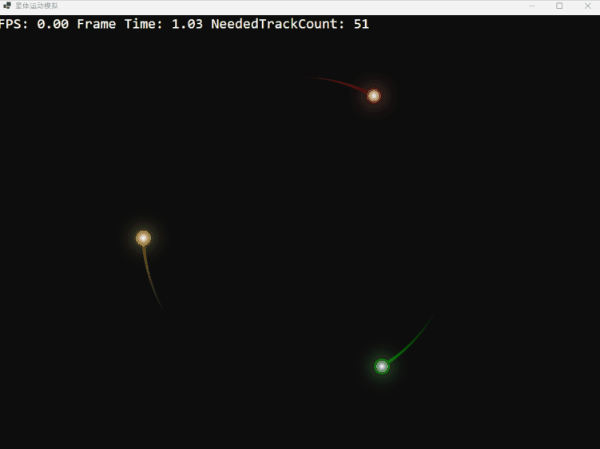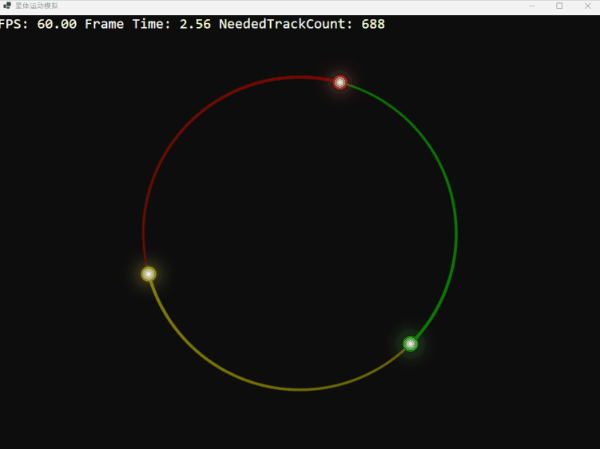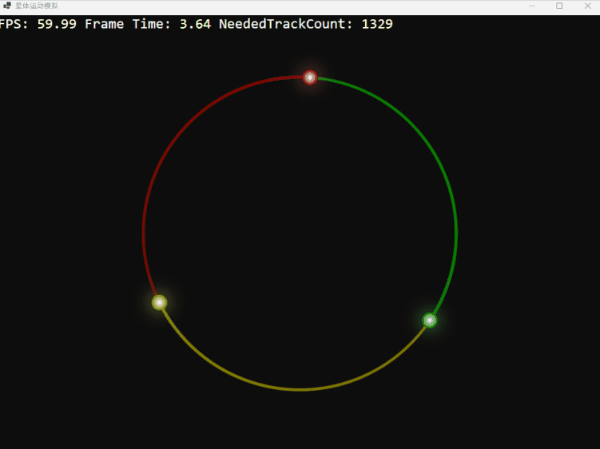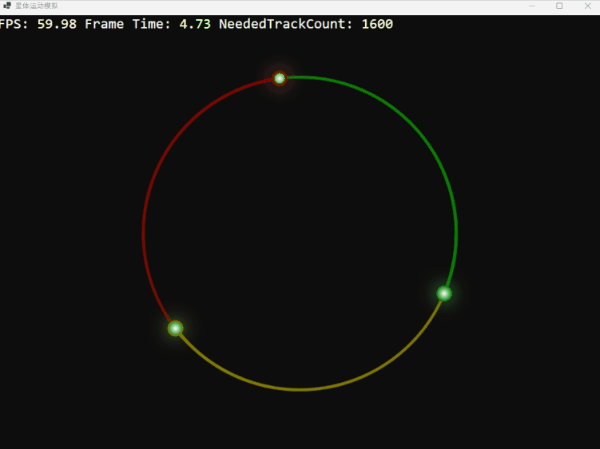
三颗星体在引力的束缚下，跳着一曲永不终结的华尔兹。这画面充满了数学和物理上的和谐之美，不是吗？

然而，这种美丽，是建立在一种极其脆弱的平衡之上的。

秩序的瞬间崩溃

在真实的宇宙中，绝对的“完美”是不存在的。任何一丝微小的扰动，都可能成为压垮这个精密系统的最后一根稻草。在我的模拟中，尽管已经使用了 ode45 这样高精度的求解器，但计算过程中累积的微小误差，足以打破这种脆弱的平衡。

于是，在一段时间的完美运行后，末日来临了：

曾经优雅的舞蹈瞬间化为混乱的挣扎，星体被无情地抛向远方。秩序在刹那间崩溃，混沌取而代之。这就是三体问题最本质的恐怖与魅力——稳定是偶然，混乱是必然。

为了更清晰地展示这种不稳定性，我们可以人为地给这个系统施加一点点“扰动”。

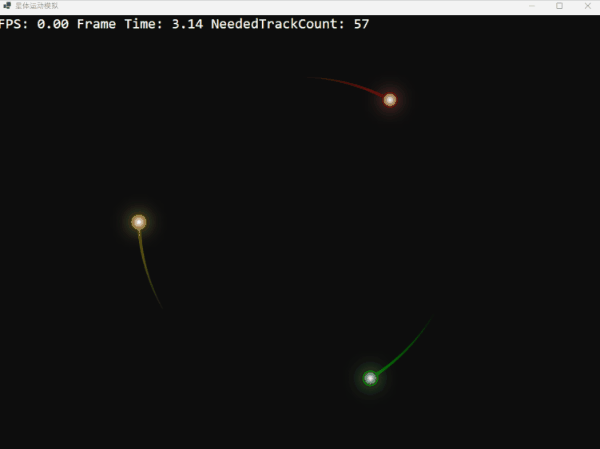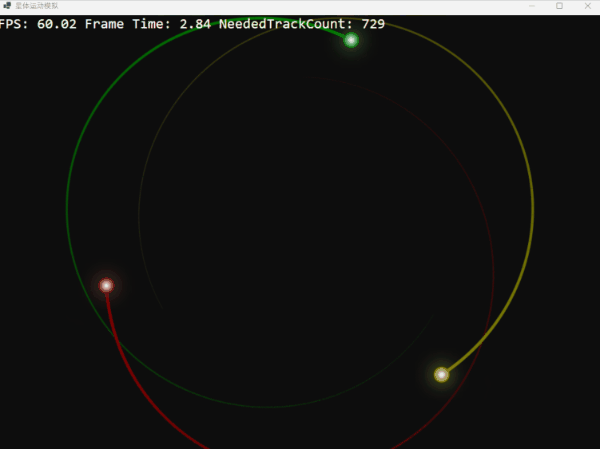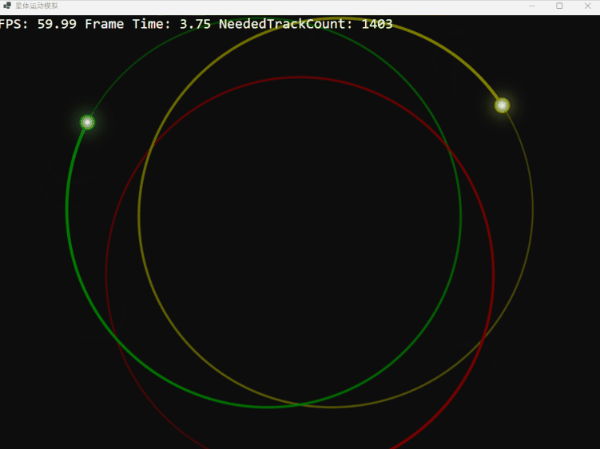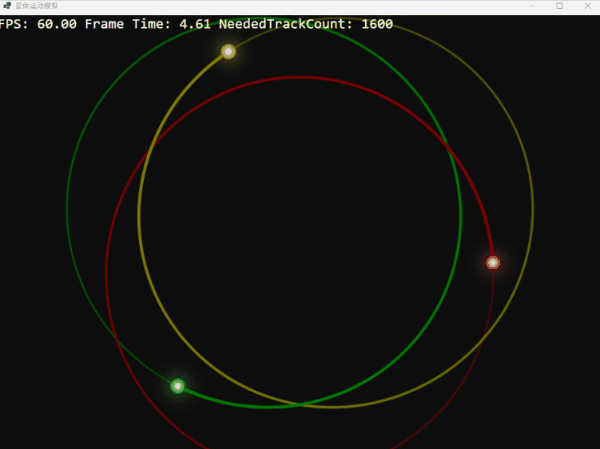
如果我们将三体的初始速度降低 10%，它们将无法维持圆形轨道，最终螺旋式地坍然后重生：

反之，如果我们将初始速度提高 10%，它们则会挣脱引力的束缚，渐行渐远，但由于失去速度最终又回归：

总结

从和谐的日地月系统，到美丽而脆弱的三体环舞，再到最终不可避免的混沌结局，我们通过代码管中窥豹，领略了宇宙法则的两个侧面：它可以创造出令人赞叹的秩序，也可以在瞬间将一切归于混乱。

这种从有序到无序的张力，正是天体运动乃至整个物理世界最迷人的地方。

感谢你阅读到这里！如果感觉本文对您有帮助，请不吝评论和点赞，这也是我持续创作的最大动力！

如果你觉得我的 N 体运行模拟项目很有趣，欢迎来 GitHub 给一个 Star ：

https://github.com/sdcb/n-body

也欢迎加入我的 .NET骚操作 QQ群：495782587，在这里我们可以一起交流 .NET 和 AI 领域各种最新、最酷、最“骚”的玩法！