von Mises Distribution (冯·米赛斯分布)的随机模拟与参数估计的笔记（二）

von Mises Distribution (冯·米赛斯分布)的随机模拟与参数估计的笔记（二）

1.参数估计算子分析

​ 在上一节中，我们讨论了von Mises Distribution的概率分布函数PDF和累计分布函数CDF，并给出了von Mises Distribution的随机模拟和参数估计matlab程序，其中在此我们就参数估计的细节进行补充。其基于最大似然参数估计算子，如下表：

​ 来源于《Statistical Distributions》

利用如下改进贝塞尔函数的关系求解参数\(\kappa\)，如下表达：

\[R=\frac{1}{n}\left[\left(\sum_{i=1}^{n} \cos x_{i}\right)^{2}+\left(\sum_{i=1}^{n} \sin x_{i}\right)^{2}\right]^{1 / 2}
\]

\[\kappa \approx \begin{cases}2 R+R^{3}+\frac{5}{6} R^{5} \quad & R<0.53 \\ -0.4+1.39 R+\frac{0.43}{1-R} & 0.53 \leq R<0.85 \\ \frac{1}{R^{3}-4 R^{2}+3 R} & \text { other }\end{cases}
\]

1.1 \(\mu\)参数估计分析matlab代码

function mu=circ_mean(alpha, w, dim)
%
% mu = circ_mean(alpha, w)
%   Computes the mean direction for circular data.
%
%   Input:
%     alpha	sample of angles in radians
%     [w		weightings in case of binned angle data]
%     [dim  compute along this dimension, default is 1]
%
%     If dim argument is specified, all other optional arguments can be
%     left empty: circ_mean(alpha, [], dim)
%
%   Output:
%     mu		mean direction

%
% PHB 7/6/2008
%
% References:
%   Statistical analysis of circular data, N. I. Fisher
%   Topics in circular statistics, S. R. Jammalamadaka et al.
%   Biostatistical Analysis, J. H. Zar
%
% Circular Statistics Toolbox for Matlab

% By Philipp Berens, 2009
% berens@tuebingen.mpg.de - www.kyb.mpg.de/~berens/circStat.html

if nargin < 3
  dim = 1;
end

if nargin < 2 || isempty(w)
  % if no specific weighting has been specified
  % assume no binning has taken place
	w = ones(size(alpha));
else
  if size(w,2) ~= size(alpha,2) || size(w,1) ~= size(alpha,1)
    error('Input dimensions do not match');
  end
end

% compute weighted sum of cos and sin of angles
r = sum(w.*exp(1i*alpha),dim);

% obtain mean by
mu = angle(r);

1.2 \(\kappa\)参数估计的matlab代码

function kappa = circ_kappa(alpha,w)
%
% kappa = circ_kappa(alpha,[w])
%   Computes an approximation to the ML estimate of the concentration
%   parameter kappa of the von Mises distribution.
%
%   Input:
%     alpha   angles in radians OR alpha is length resultant
%     [w      number of incidences in case of binned angle data]
%
%   Output:
%     kappa   estimated value of kappa
%
%   References:
%     Statistical analysis of circular data, Fisher, equation p. 88
%
% Circular Statistics Toolbox for Matlab

% By Philipp Berens, 2009
% berens@tuebingen.mpg.de - www.kyb.mpg.de/~berens/circStat.html

alpha = alpha(:);

if nargin<2
  % if no specific weighting has been specified
  % assume no binning has taken place
	w = ones(size(alpha));
else
  if size(w,2) > size(w,1)
    w = w';
  end
end

N = length(alpha);

if N>1
  R = circ_r(alpha,w);
else
  R = alpha;
end

if R < 0.53
  kappa = 2*R + R^3 + 5*R^5/6;
elseif R>=0.53 && R<0.85
  kappa = -.4 + 1.39*R + 0.43/(1-R);
else
  kappa = 1/(R^3 - 4*R^2 + 3*R);
end

if N<15 && N>1
  if kappa < 2
    kappa = max(kappa-2*(N*kappa)^-1,0);
  else
    kappa = (N-1)^3*kappa/(N^3+N);
  end
end

function r = circ_r(alpha, w, d, dim)
% r = circ_r(alpha, w, d)
%   Computes mean resultant vector length for circular data.
%
%   Input:
%     alpha	sample of angles in radians
%     [w		number of incidences in case of binned angle data]
%     [d    spacing of bin centers for binned data, if supplied
%           correction factor is used to correct for bias in
%           estimation of r, in radians (!)]
%     [dim  compute along this dimension, default is 1]
%
%     If dim argument is specified, all other optional arguments can be
%     left empty: circ_r(alpha, [], [], dim)
%
%   Output:
%     r		mean resultant length
%
% PHB 7/6/2008
%
% References:
%   Statistical analysis of circular data, N.I. Fisher
%   Topics in circular statistics, S.R. Jammalamadaka et al.
%   Biostatistical Analysis, J. H. Zar
%
% Circular Statistics Toolbox for Matlab

% By Philipp Berens, 2009
% berens@tuebingen.mpg.de - www.kyb.mpg.de/~berens/circStat.html

if nargin < 4
  dim = 1;
end

if nargin < 2 || isempty(w)
  % if no specific weighting has been specified
  % assume no binning has taken place
	w = ones(size(alpha));
else
  if size(w,2) ~= size(alpha,2) || size(w,1) ~= size(alpha,1)
    error('Input dimensions do not match');
  end
end

if nargin < 3 || isempty(d)
  % per default do not apply correct for binned data
  d = 0;
end

% compute weighted sum of cos and sin of angles
r = sum(w.*exp(1i*alpha),dim);

% obtain length
r = abs(r)./sum(w,dim);

% for data with known spacing, apply correction factor to correct for bias
% in the estimation of r (see Zar, p. 601, equ. 26.16)
if d ~= 0
  c = d/2/sin(d/2);
  r = c*r;
end

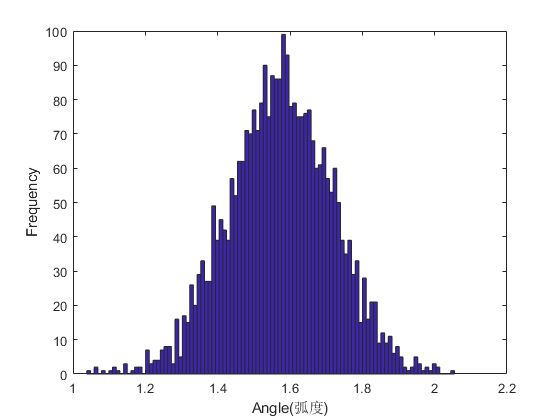
2 代码效果分析

clc
clear all
close all

theta=pi/2;  %设置模拟参数
kappa=50;
n=3000;

alpha=circ_vmrnd(theta,kappa,n);  %生成制定参数的von-Mises分布的随机数

[thetahat1 kappa1]=circ_vmpar(alpha); %对其进行分布参数进行估计分析

 %绘制模拟数据直方图
figure(1)
hist(alpha,100);
xlabel('Angle(弧度)');
ylabel('Frequency');

X = categorical({'Really value','Estimate value'});

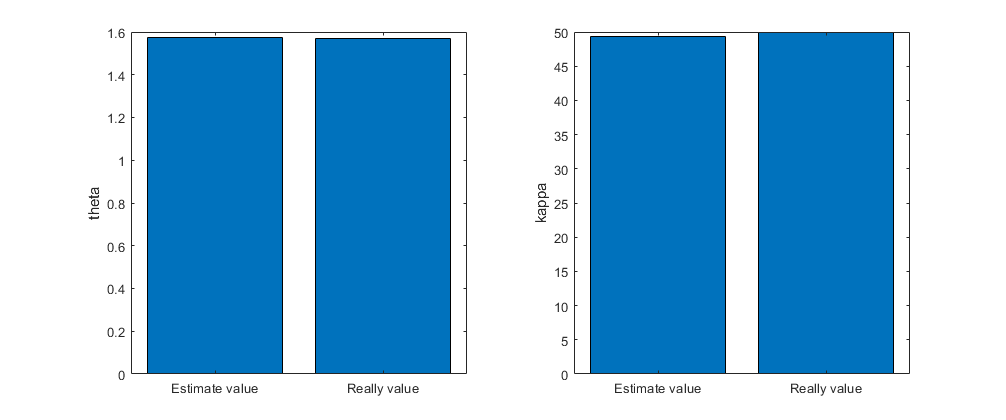
 %估计参数与模型参数对比
figure(2)
subplot(1,2,1)
bar(X,[theta,thetahat1]);
ylabel('theta');

subplot(1,2,2)
bar(X,[kappa,kappa1]);
ylabel('kappa');