Rosenblatt感知器

一、定义

Rosenblatt感知器建立在一个线性神经元之上，神经元模型的求和节点计算作用于突触输入的线性组合，同时结合外部作用的偏置，对若干个突触的输入项求和后进行调节。

二、基本计算过程

Rosenblatt感知器的基本计算步骤如下：

（1）将数据作为输入送入神经元。

（2）通过权值和输入共同计算诱导局部域，诱导局部域是指求和节点计算得到的结果，计算结果如下：

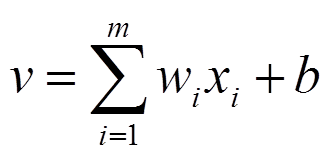
（3）以硬限幅器为输出函数，诱导局部域被送入硬限幅器，形成最终的输出硬限幅器的工作原理如下。

硬限幅器输入为正时，神经元输出+1，反之输出为-1.计算公式为：

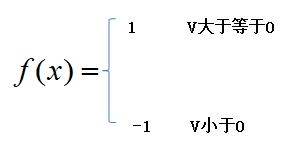
三、权值修正

首先，会产生一个初始权值，由初始权值计算得到的输出结果肯定有误差。接着，要想办法让误差减少，这个过程就是权值w修正的过程。

权值修正有单样本修正算法和批量修正算法

单样本修正算法的步骤为：神经网络每次读入一个样本，进行修正，样本读取完毕，修正过程结束。算法过程描述如下：

（1）设置如下参数：

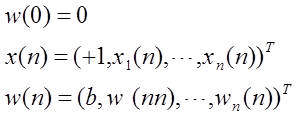
其中，b为偏置，x为输入向量，w为权值。

(2)感知器激活

对于每个时间步n,通过输入向量x(n)和期望输出d(n)激活感知器。

（3）计算感知器的输出。

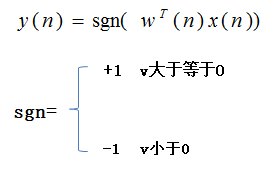
其中，n为时间步，x(n)为输入向量，w(n)为权值向量，sgn为硬限幅函数，v为硬限幅函数的输入值

（4）更新感知器的权值向量

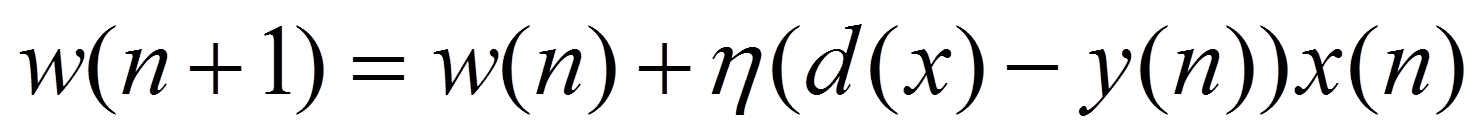
其中，n为学习速率,调整更新的步伐。

用Python实现上述算法。代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Jun 10 10:41:14 2015

@author: chaofn
"""
import numpy as np
b=0
a=0.5
x=np.array([[b,1,1],[b,1,0],[b,0,0],[b,0,1]])
d=np.array([1,1,0,1])
w=np.array([b,0,0])
def sgn(v):
    if v>0:
        return 1
    else:
        return 0
def comy(myw,myx):
    return sgn(np.dot(myw.T,myx))
def neww(oldw,myd,myx,a):
    return oldw+a*(myd-comy(oldw,myx))*myx
i=0
for xn in x:
    w=neww(w,d[i],xn,a)
    i+=1
    print(w)
for xn in x:
    print("%d and %d => %d"%(xn[1],xn[2],comy(w,xn)))