Vijos P1448 校门外的树【多解，线段树，树状数组，括号序列法+暴力优化】

校门外的树

描述

校门外有很多树，有苹果树，香蕉树，有会扔石头的，有可以吃掉补充体力的……
如今学校决定在某个时刻在某一段种上一种树，保证任一时刻不会出现两段相同种类的树，现有两个操作：
K=1，K=1，读入l、r表示在区间[l,r]中种上一种树，每次操作种的树的种类都不同
K=2，读入l,r表示询问l~r之间能见到多少种树
（l,r>0）

格式

输入格式

第一行n,m表示道路总长为n，共有m个操作
接下来m行为m个操作

输出格式

对于每个k=2输出一个答案

样例1

样例输入1

5 4
1 1 3
2 2 5
1 2 4
2 3 5

样例输出1

1
2

限制

1s

提示

范围：20%的数据保证，n,m<=100
60%的数据保证，n <=1000,m<=50000
100%的数据保证，n,m<=50000

来源

dejiyu@CSC WorkGroup

题目链接：https://vijos.org/p/1448

分析：这题目从上午九点写到下午四点，历经七个小时的磨难，只为给大家提供最优质的方法！

这道题我用了三种方法去解决！

第一种：线段树【时间花费最长，也最伤脑的写法】，做法是将[a,b]种上一种树，这个修改操作影响的询问满足，

询问区间与[a,b]有交，转化为统计总修改数-与某询问交为空集的修改数

对于一个修改操作[l,r]，与它为空集的询问[a,b]满足a∈[1,l-1]或者b∈[r+1,n]

用两棵线段树维护，修改[l,r]，将第一棵的[1,l-1]区间+1，第二棵[r+1,n]区间+1

询问[a,b]，答案为之前的修改数-（第一棵单点询问b+第二棵单点询问a）

代码中线段树结点的l，r其实就是两棵线段树。。。标记永久化

下面给出线段树的代码：

 #include <bits/stdc++.h>
 using namespace std;
 const int N=;
 int n,m;
 inline int read()
 {
     int x=,f=;
     char ch=getchar();
     while(ch<''||ch>'')
     {
         if(ch=='-')
             f=-;
         ch=getchar();
     }
     while(ch>=''&&ch<='')
     {
         x=x*+ch-'';
         ch=getchar();
     }
     return x*f;
 }
 inline void write(int x)
 {
     if(x<)
     {
         putchar('-');
         x=-x;
     }
     if(x>)
     {
         write(x/);
     }
     putchar(x%+'');
 }
 struct Tree
 {
     int l,r;
     int left,right;
 }tree[N<<];
 inline void buildtree(int x,int y,int pos)
 {
     tree[pos].left=x;
     tree[pos].right=y;
     if(x==y)
     {
         return;
     }
     int mid=(x+y)/;
     buildtree(x,mid,pos*);
     buildtree(mid+,y,pos*+);
 }
 inline void insertl(int x,int y,int pos)
 {
     int l=tree[pos].left;
     int r=tree[pos].right;
     if(l==x&&r==y)
     {
         tree[pos].l++;
         return;
     }
     int mid=(l+r)/;
     if(y<=mid)
         insertl(x,y,pos*);
     else if(x>mid)
         insertl(x,y,pos*+);
     else
     {
         insertl(x,mid,pos*);
         insertl(mid+,y,pos*+);
     }
 }
 inline void insertr(int x,int y,int pos)
 {
     int l=tree[pos].left;
     int r=tree[pos].right;
     if(l==x&&r==y)
     {
         tree[pos].r++;
         return;
     }
     int mid=(l+r)/;
     if(y<=mid)
         insertr(x,y,pos*);
     else if(x>mid)
         insertr(x,y,pos*+);
     else
     {
         insertr(x,mid,pos*);
         insertr(mid+,y,pos*+);
     }
 }
 inline int askl(int k,int x)
 {
     int l=tree[k].left;
     int r=tree[k].right;
     if(l==r)
         return tree[k].l;
     int mid=(l+r)/;
     if(x<=mid)
         return tree[k].l+askl(k*,x);
     else return tree[k].l+askl(k*+,x);
 }
 inline int askr(int k,int x)
 {
     int l=tree[k].left;
     int r=tree[k].right;
     if(l==r)
         return tree[k].r;
     int mid=(l+r)/;
     if(x<=mid)
         return tree[k].r+askr(k*,x);
     else return tree[k].r+askr(k*+,x);
 }
 int main()
 {
     n=read();
     m=read();
     int tot=;
     buildtree(,n,);
     for(int i=;i<=m;i++)
     {
         int t,a,b;
         cin>>t>>a>>b;
         if(t==)
         {
             insertl(,a-,);
             insertr(b+,n,);
             tot++;
         }
         else
         {
             int ans=askr(,a)+askl(,b);
             write(tot-ans);
             cout<<endl;
         }
     }
     return ;
 }

第二种写法：树状数组

做法：这题是一条条线段，所以我们可以用线段树之类的东东来实现，然后感觉树状数组写起来简单一点所以就打了
开两个数组来存一个是开始的点的数量，一个是结束的 ，然后随便搞一下，最后输出就可以了

下面给出树状数组写法：

 #include <bits/stdc++.h>
 using namespace std;
 const int N=;
 int l[N],r[N];
 int n,m;
 inline int read()
 {
     int x=,f=;
     char ch=getchar();
     while(ch<''||ch>'')
     {
         if(ch=='-')
             f=-;
         ch=getchar();
     }
     while(ch>=''&&ch<='')
     {
         x=x*+ch-'';
         ch=getchar();
     }
     return x*f;
 }
 inline void write(int x)
 {
     if(x<)
     {
         putchar('-');
         x=-x;
     }
     if(x>)
     {
         write(x/);
     }
     putchar(x%+'');
 }
 int lowbit(int x)
 {
     return x&-x;
 }
 void add(int x,int d,int c[])
 {
     while(x<=n)
     {
         c[x]+=d;
         x+=lowbit(x);
     }
 }
 int sum(int x,int c[])
 {
     int s=;
     while(x>)
     {
         s+=c[x];
         x-=lowbit(x);
     }
     return s;
 }
 int main()
 {
     int k,x,y;
     n=read();
     m=read();
     for(int i=;i<=m;i++)
     {
         cin>>k>>x>>y;
         if(k==)
         {
             add(x,,l);
             add(y,,r);
         }
         else
         {
             write(sum(y,l)-sum(x-,r));
             cout<<endl;
         }
     }
     return ;
 }

第三种方法：括号序列法【简称括号法】

假设有一个长度为10的数轴，我们要将区间[ 2 , 5 ]中种树，这时，我们将 2 处放一个左括号 " ( "  ,5处放一个 " )"  ，表示区间 [ 2 , 5 ]种了树。

查询某个区间树的种类，如区间[ 3 , 10]，只需统计10之前（包括10）有多少个‘（’，统计3之前有多少个‘）’，（不包括3）。  

如下图所示：

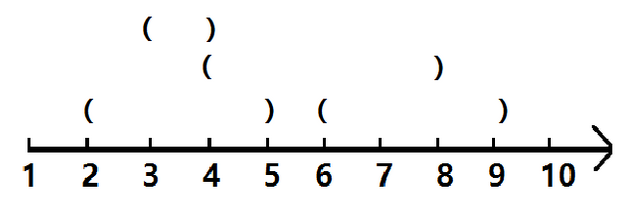
以上就是括号序列的过程。简单的说，就是更新区间[a,b]时，点a记录左括号数，点b记录右括号数，查询区间[a,b]时，即为b之前（包括b）的左括号数-a之前的右括号数。

下面给出非常简练优秀的代码：

 #include <bits/stdc++.h>
 using namespace std;
 const int N=;
 int l[N],r[N];
 int n,m;
 inline int read()
 {
     int x=,f=;
     char ch=getchar();
     while(ch<''||ch>'')
     {
         if(ch=='-')
             f=-;
         ch=getchar();
     }
     while(ch>=''&&ch<='')
     {
         x=x*+ch-'';
         ch=getchar();
     }
     return x*f;
 }
 inline void write(int x)
 {
     if(x<)
     {
         putchar('-');
         x=-x;
     }
     if(x>)
     {
         write(x/);
     }
     putchar(x%+'');
 }
 int main()
 {
     int k,x,y;
     n=read();
     m=read();
     for(int i=;i<=m;i++)
     {
         cin>>k>>x>>y;
         if(k==)
         {
             for(int j=x;j<=n;j+=j&-j)
                 l[j]++;
             for(int j=y;j<=n;j+=j&-j)
                 r[j]++;
         }
         else
         {
             int ans=;
             for(int j=y;j;j-=j&-j)
                 ans+=l[j];
             for(int j=x-;j;j-=j&-j)
                 ans-=r[j];
             write(ans);
             cout<<endl;
         }
     }
     return ;
 }