关于逆元的概念、用途和可行性的思考（附51nod 1013 和 51nod 1256）

【逆元的概念】

逆元和单位元这个概念在群中的解释是：  逆元是指数学领域群G中任意一个元素a，都在G中有唯一的逆元a'，具有性质a×a'=a'×a=e，其中e为该群的单位元。

群的概念是：  如果独异点（幺半群）中每一个元素都有逆元，那么这个独异点（幺半群）叫做群。

独异点（幺半群）：  有单位元的半群。

半群：  可结合的代数系统。即 ，有 。

代数系统：我的理解是代数系统包含一个数的集合A和至少一个运算规则，所有的运算都是封闭的，不会产生不在A集合中的数。

我们知道的实数集合R和加减乘除等一系列运算规则就组成了一个代数系统。根据上面的概念我们当然知道这是一个群。

简单来说：对于任意群中元素a,b，如果a*b = 1 ，那么a就是b的左逆元，b就是a的右逆元。（如果这个群满足交换律，这个群就是交换群，那么a和b互为逆元。）

这里有一个例题，就是求逆元的：

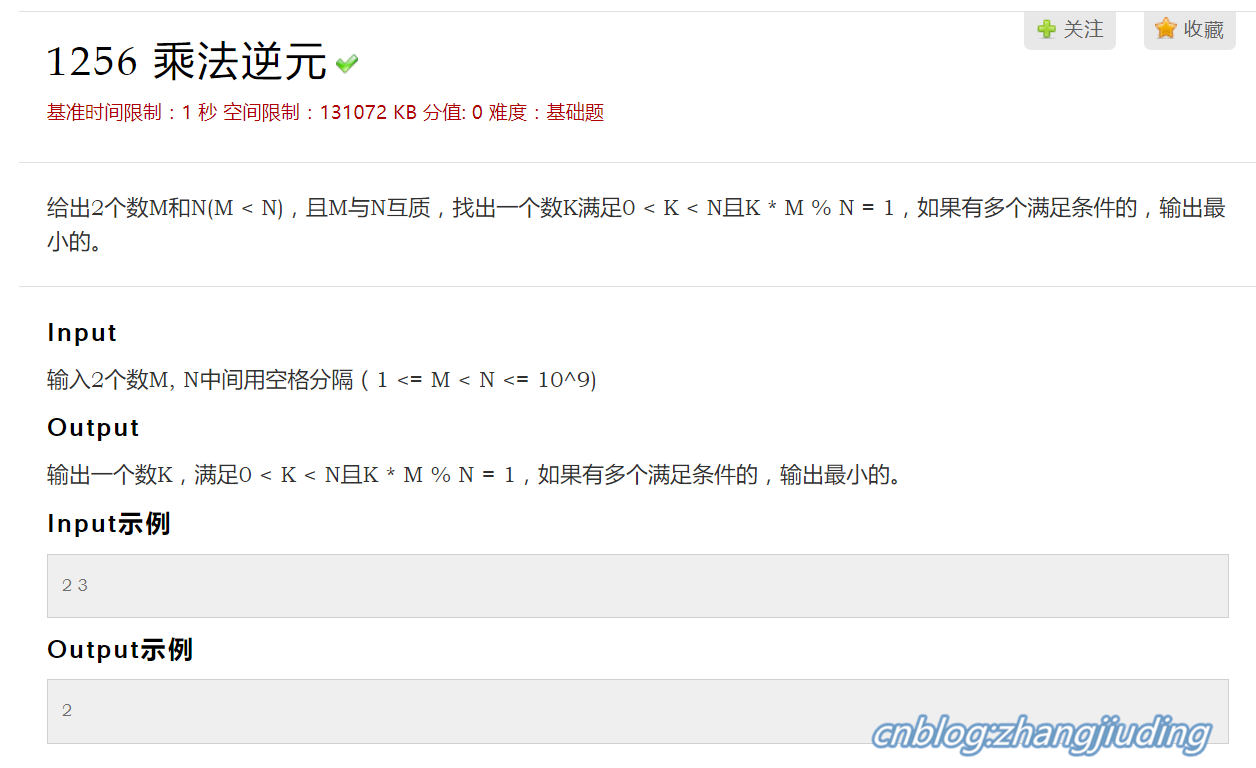
当然这是一道单纯求逆元的题。

　　 （K*M）% N = 1

看到这个我们想把%消掉，看起来就会简单了。

==>   (K*M-1)%N = 0

==>   K*M-1 = S*N (S为未知数)

现在我们成功的消掉了%，这个等式只有K和S两个未知数。

如果还没看出来的话，我们把K换成x，S换成y，再移项看看：

==>    M*x - N*y = 1

是不是很熟悉，对，就是拓展欧几里得。

ll gcd(ll a,ll b,ll &x,ll &y){
    if (b==){
        x=,y=;
        return a;
    }
    ll q=gcd(b,a%b,y,x);
    y-=a/b*x;
    return q;
}

这样能够解出x,y的一对解，再把它移到适合的范围内就得到了我们的结果。

这题的代码如下：

#include <iostream>
#include <algorithm>
#include <string>
#include <stdio.h>
#include <string.h>
#include <math.h>
#define rep(u,i,n) for(int u = i;u <= n; u++)
typedef long long ll;
using namespace std;
ll gcd(ll a,ll b,ll &x,ll &y){
    if (b==){
        x=,y=;
        return a;
    }
    ll q=gcd(b,a%b,y,x);
    y-=a/b*x;
    return q;
}
int main() {
  ll n,m,x = ,y = ;
  while(cin >> m >> n){
    gcd(n,m,x,y);
    if(y > ) cout << y << endl;
    else cout << n+y << endl;
  }
  return ;
}

【逆元的用途】 除法取模

我们知道 (a*b)%n = c --> ((a%n)*(b%n))%n = c;

但是(a/b)%n 该怎么求呢？

如果n = 11, a = 3, b = 10 的话，直接算会导致结果错误(3/10)%11 = 0。

我们知道3/10是有值的，但是直接算结果会变成0，肯定出了某种错误。

这个错误我们暂时不做讨论，着重解决问题。

这时乘法逆元就派上用场了我们知道(3/10)%11 ==> (3*(1/10))%11

而1/10在乘法上是10的逆元(mod n = 11)，意思就是我们用10的逆元取代1/10的位置就可以解决了。

(3/(10的逆元))%11就是我们要的结果。

于是我们成功的解决了除法时取模的问题。

这里有一个例题：

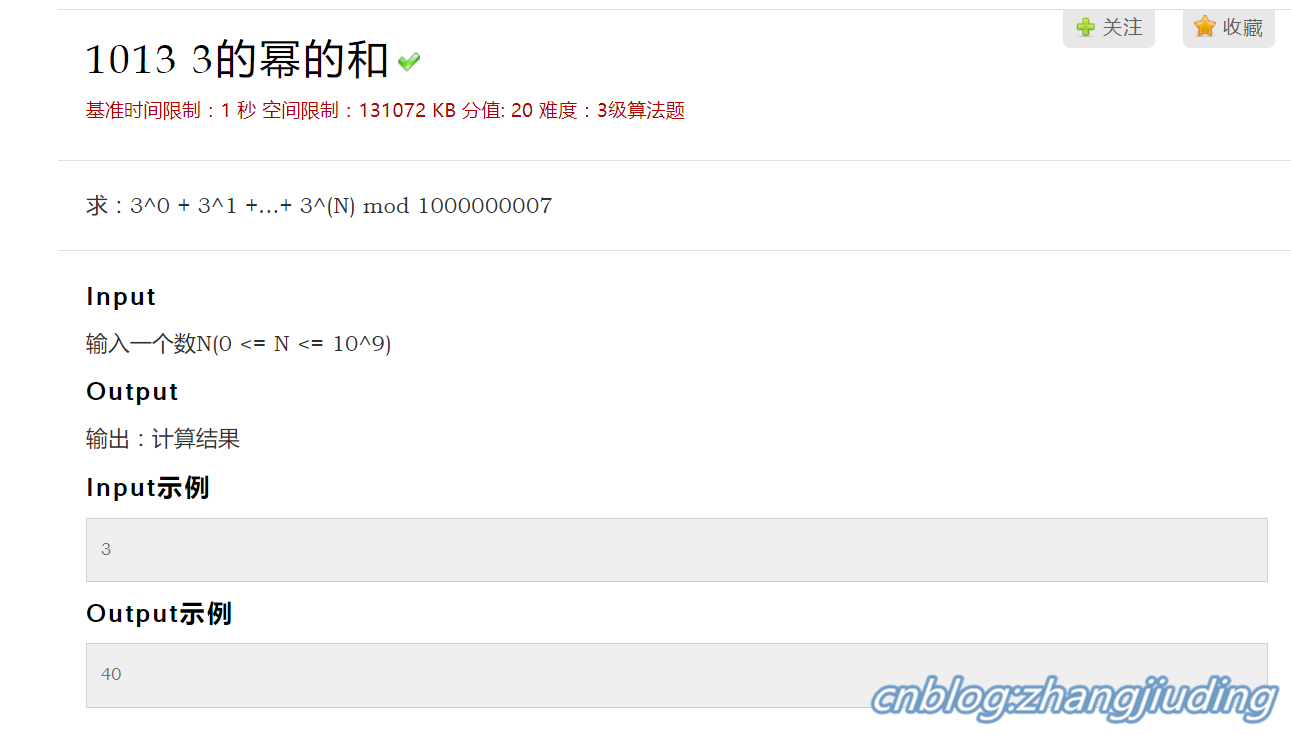
这个逆元是手动求的，懒得写求逆元代码。

代码如下：

#include <bits\stdc++.h>
typedef long long ll;
using namespace std;
const int mod = ;
ll mod_pow(ll x,ll n)
{
  ll ans = ;
  while(n > ) {
    if(n %  == ){
        ans = ans * x % mod;
        }
        n /= ;
        x = x*x % mod;
  }
  return ans;
}
int main()
{
  ll n,ans;
  cin >> n;
  n++;
  ans = (mod_pow(,n)-)*%mod; // 500000004是2对mod的逆元 ，逆元在除以后取模时使用
  cout << ans << endl;
  return ;
}