自动微分方法(auto diff)

学习机器学习的同学在学习过程中会经常遇到一个问题，那就是对目标函数进行求微分，线性回归这类简单的就不说、复杂的如神经网络类那些求导过程的酸爽。像我还是那种比较粗心的人往往有十导九错，所以说自动求导就十分有必要了，本文主要介绍几种求导的方式。假设我们的函数为$f(x,y)=x^2y+y+2$，目标是求出偏导$\frac{\partial{f}}{\partial{x}}$和$\frac{\partial{f}}{\partial{y}}$。求导的方式主要分为以下几种

手动求导法(Manual Differentiation)###

首先准备一张纸和一支笔，根据上学时候学到的求导法则，开始计算。最终得到的结果

$\frac{\partial{f}}{\partial{x}}=2xy$

$\frac{\partial{f}}{\partial{y}}=x^2+1$

上面这个小例子比较简单，口算即可得到答案，但如果方程比较复杂那就难说了。幸好有自动求导的方法，例如符号求导方法。

符号求解法(Symbolic Differentiation)###

符号求导是根据一些求导法则，进行求导。例如我们大学高数学习的$(uv)\prime=u'v+v'u$，$(u+v)'=u'+v'$，$(\frac{u}{v})'=\frac{u'v-v'u}{v^2}$等等，下图是$g(x,y)=5+xy$的符号求导工作流程。

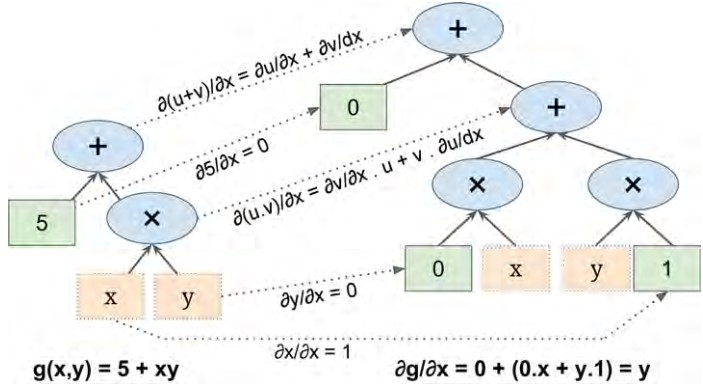
原公式在图的左边，求导公式在图的右半部分，求导的过程是先求叶子节点，自下向上。最终对节点进行见之得到求导结果$\frac{\partial{g}}{\partial{x}}=y$，这个例子固然简单，但是对于一个更复杂的公式，那么求导符号图将会十分的庞大(表达式膨胀)，另外对于一些变化的公式（硬代码）这种方法就无能为力了：

def fun(a,b):

    z=0

    for i in range(100):

        z = a * np.cos(z + i) + z * np.sin(b - i)

    return z

数值求导法(Numerical Differentiation)###

导数的定义是当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。

其中$\varepsilon$是一个无穷小的数，所以我们可以计算在x=3,y=4这一点对x的偏导数，$f'(x=3,y)=\frac{f(3+\varepsilon,4)-f(3,4)}{\varepsilon}$，对应的代码如下：

def f(x, y):

    return x**2*y + y + 2

def derivative(f, x, y, x_eps, y_eps):

    return (f(x + x_eps, y + y_eps) - f(x, y)) / (x_eps + y_eps)

df_dx = derivative(f, 3, 4, 0.00001, 0)

df_dy = derivative(f, 3, 4, 0, 0.00001)

>>print(df_dx)

24.000039999805264

>>print(df_dy)

10.000000000331966

通过上面的结果我们发现，得出的结果不是十分的精确，并且在对x和y求偏导的整个过程中，至少需要计算3次$f()$，也就是说如果有1000个参数，那么至少需要计算1001次$f()$，在神经网络中，参数巨多，这样计算效率会比较差。不过这种方法常被用到进行检验得到的求导结果是否正确。

前向自动求导法(Forward-Mode Autodiff)###

前向求导是依赖于数值求导和符号求导的一种求解方法，给定公式$a+{\varepsilon}b$，这种被称作dual number,其中a和b是实数，$\varepsilon$是一个无穷小的数，并且${\varepsilon}^2=0$，举个栗子，$42 + 24\varepsilon$，我们可以把它看成42.00000000...24的数值.我们可以通过这种方法(42.0,24.0)来表示，dual number满足以下的运算法则：

1.$\lambda(a+b\varepsilon) = a\varepsilon + b{\lambda}\varepsilon$
2.$(a+b\varepsilon)+(c+d\varepsilon) = (a+c)+(b+d)\varepsilon$
3.$(a+b\varepsilon)\times(c+d\varepsilon) = ac+(ad+bc)\varepsilon+(bd){\varepsilon}^2=ac+(ad+bc)\varepsilon$

还有一点就是$h(a+b\varepsilon)=h(a)+b{\times}h'(a)\varepsilon$。

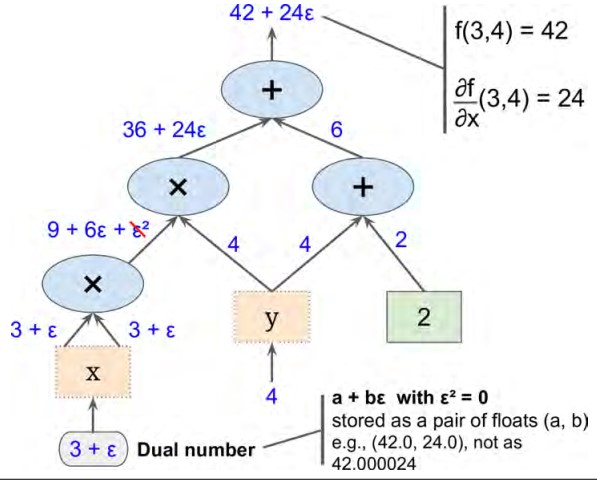
上图给出了使用前向求导方法计算出$f(x,y)$在x=3，y=4这一点$\frac{\partial{f}}{\partial{x}}(3,4)$的偏导，同理求出$\frac{\partial{f}}{\partial{y}}(3,4)$,图中的思路很清晰就不赘述。前向求导方法相对数值求导来说准确率较高，当和数值求导方法一样如果参数过多的时候效率会比较差，因为这种方法需要遍历整个图。

逆向自动求导法(Reverse-Mode Atuodiff)###

TensorFlow采用的是逆向自动求导方法，该方法首先正向遍历整个图，计算出每个节点的值；然后逆向(从上到下)遍历整个图，计算出节点的偏导值，步骤如下图所示；节点内蓝色的数值表示正向计算出的结果，为了方便表达，我们从下到上，从左到右依次标注为$n_1$到$n_7$，可以看到最后的值$n_7$(顶部节点)为42。

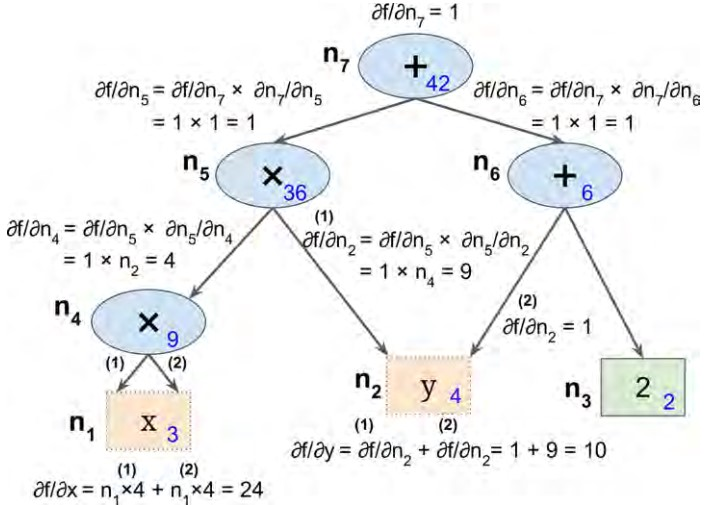
在逆向求导过程中使用链式求导方法：

$\frac{\partial{f}}{\partial{x}}=\frac{\partial{f}}{\partial{n_i}}{\times}\frac{\partial{n_i}}{\partial{x}}$

先看节点$n_7$，作为输出节点$f=n_7$，所以导数值为$\frac{\partial{f}}{\partial{n_7}}=1$,

接着向下计算$n_5$，$\frac{\partial{f}}{\partial{n_5}}=\frac{\partial{f}}{\partial{n_7}}{\times}\frac{\partial{n_7}}{\partial{n_5}}$，上一步计算出$\frac{\partial{f}}{\partial{n_7}}=1$，现在我们只需要计算$\frac{\partial{n_7}}{\partial{n_5}}$，从图中我们知道$n_7=n_5+n_6$，可以得出$\frac{\partial{f}}{\partial{x}}=1$。所以$\frac{\partial{f}}{\partial{n_5}}=1$，接下来的步骤可以看上面的图，这里就不赘述了。

逆向自动求导法这种方法十分强大且准确率较高，尤其是有却多的输入。这种发方法仅需要正向和逆向遍历一次即可，这种方法更强大的地方在于能够解决符号求解法中硬代码的问题。