Noip模拟49 2021.9.7

T1 reverse

又一道板子打假的挂分题，直接挂到倒二。。

考场上思路神奇，居然想到用$bfs$建边然后跑最短路，

其实当时也想到了直接$bfs$，但是不知道为啥觉得$dij$屌就没直接打$bfs$。。。

最可怕的是$dji$没打对，以后可能要早操背板子了。。。

然后其实这题能卡过，因为$k$都特别小。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 namespace AE86{
 4     inline int read(){
 5         int x=0,f=1;char ch=getchar();
 6         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 7         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 8     }inline void write(int x,char opt='\n'){
 9         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
10         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
11         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
12 }using namespace AE86;
13
14 inline int max(int a,int b){return a>b?a:b;}
15 inline int min(int a,int b){return a<b?a:b;}
16
17 int n,k,m,s,ans[100005],pos,wei,l,r;
18 bool vis[100005];
19 double mid;
20 int q[100005],h=0,t=0;
21 namespace WSN{
22     inline short main(){
23         // freopen("reverse3.in","r",stdin);
24         // freopen("bl.out","w",stdout);
25         n=read(); k=read(); m=read(); s=read();
26         for(register int i=1;i<=n;++i) ans[i]=-1;
27         for(register int i=1,jz;i<=m;++i)
28             jz=read(),vis[jz]=1,ans[jz]=-1;
29         q[++t]=s; ans[s]=0; vis[s]=1;
30         while(h<=t){
31             pos=q[h++];
32             l=max(1,pos-k+1); r=min(pos,n-k+1);
33             for(register int i=l;i<=r;++i){
34                 wei=i+(k-(pos-i+1));
35                 if(!vis[wei]){
36                     ans[wei]=ans[pos]+1;
37                     vis[wei]=1;
38                     q[++t]=wei;
39                 }
40             }
41         }
42         for(register int i=1;i<=n;++i)
43             write(ans[i],' ');
44         return 0;
45     }
46 }
47 signed main(){return WSN::main();}

卡常暴力

然后正解能优化到$O(n)$，就是使用一个链表，

发现每个$1$每次挪动的位置奇偶性都是一样的，那么初始化链表为$nxt_i=i+2$

然后$bfs$每次循环的时候直接找能跳到的位置并把链表指针指向循环最后一个元素。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 namespace AE86{
 4     inline int read(){
 5         int x=0,f=1;char ch=getchar();
 6         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 7         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 8     }inline void write(int x,char opt='\n'){
 9         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
10         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
11         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
12 }using namespace AE86;
13
14 inline int max(int a,int b){return a>b?a:b;}
15 inline int min(int a,int b){return a<b?a:b;}
16
17 int n,k,m,s,ans[100005],pos,l,r,nxt[100005],wei,nt;
18 bool vis[100005];
19 int q[100005],h=0,t=0;
20 namespace WSN{
21     inline short main(){
22         n=read(); k=read(); m=read(); s=read();
23         for(register int i=1;i<=n;++i) ans[i]=-1;
24         for(register int i=1;i<=m;++i) vis[read()]=1;
25         q[++t]=s; ans[s]=0; vis[s]=1;
26         for(int i=1;i<=n;i++) nxt[i]=i+2;
27         while(h<=t){
28             pos=q[h++]; l=max(1,pos-k+1); r=min(pos,n-k+1);
29             wei=l*2+k-pos-1;
30             while(wei<=r*2+k-pos-1){
31                 nt=nxt[wei]; nxt[wei]=nxt[r*2+k-pos-1];
32                 if(!vis[wei]) ans[wei]=ans[pos]+1,vis[wei]=1,q[++t]=wei;
33                 wei=nt;
34             }
35         }
36         for(register int i=1;i<=n;++i) write(ans[i],' ');
37         return 0;
38     }
39 }
40 signed main(){return WSN::main();}

O(n)

T2 Silhouette

首先可以看出俯视图是$min(a_i,b_j)$，就是说每个点叠最多只有那么多块。

然后发现对于给出数组排序前后计算的答案一样，证明见  这里

然后这样我们对于每一段$S$相同的区域分别处理，这一块区域之可能是矩形或者"L"形

为了不让每一列相互影响，我们假设$f_i$表示至少有$i$行没有一个块的高度等于$S$，那么对于$f_0$可以容斥出来

考虑$f_i$如何计算：

$f_i=C_{a}^{i}*(S^i*((S+1)^{a-i}-S^{a-i}))^b$

这个柿子是对于第一块（也就是$S$是矩形）的情况。

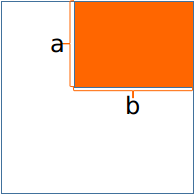
（好吧这是粘别人的）

从$a$行里面选择$i$行不合法（就是没有一个块的高度等于$S$）， $C_{a}^{i}$

然后对于每一列里面有$i$行只能选择$[0~S-1]$中的数，$S^i$

剩下的$a-i$行随便选，然后减去那一行不是$S$的情况 $(S+1)^{a-i}-S^{a-i}$

共有$b$列并且互不影响。

然后看普遍情况

有以上三种，其中后两种都可以按特殊情况告搞

考虑"L"形：分开搞

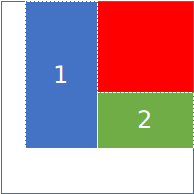
对于矩形的两种情况，无非就是没有了那一部分，可以认为举行是一种特殊的L行。

为方便，我们不妨将L行区域按如下图方式标号：

$f_i=C_a^i*(S^i*((S+1)^{a+c-i}-S^{a+c-i}))^b*(S^i*(S+1)^{a-i})^d$

因为上图中红色区域已经处理完毕，

所以对于蓝色区域，其已经满足行，而没有满足列，

对于绿色区域，其已经满足列，没有满足行

关于组合数，因为前面的$c$已经处理过，是合法的，所以我们只考虑在$a$行中选择不和法行，处理$1$区域与特殊部分同理。

然后处理绿色的$2$部分，这一部分列已经满足，所以关于特殊部分里面的减去一个$S^{a-i}$来保证合法就没有必要了

于是就直接$*(S^i*(S+1)^{a-i})^d$就可以了

这些东西都懂了代码就没什么了，很好理解。

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 namespace AE86{
 5     inline int read(){
 6         int x=0,f=1;char ch=getchar();
 7         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 8         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 9     }inline void write(int x,char opt='\n'){
10         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
11         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
12         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
13 }using namespace AE86;
14
15 const int NN=1e5+5,mod=1e9+7;
16 int n,a[NN],b[NN],m[NN<<1],has,ans=1;
17 int h[NN],v[NN];
18 inline int qmo(int a,int b){int ans=1,c=mod;a%=c;while(b){if(b&1)ans=ans*a%c;b>>=1;a=a*a%c;}return ans;}
19 inline void pre(){
20     h[0]=h[1]=1; v[0]=v[1]=1;
21     for(int i=2;i<=100000;i++) h[i]=h[i-1]*i%mod;
22     v[100000]=qmo(h[100000],mod-2);
23     for(int i=99999;i>=2;i--) v[i]=v[i+1]*(i+1)%mod;
24 }
25 inline int C(int n,int m){
26     if(n<m||n<0||m<0) return 0;
27     return h[n]*v[n-m]%mod*v[m]%mod;
28 }
29
30 inline int calc(int a,int b,int c,int d,int s,int ans=0){
31     for(int i=0;i<=a;i++){
32         int res=C(a,i)*qmo(qmo(s,i)*((qmo(s+1,a+c-i)-qmo(s,a+c-i)+mod)%mod)%mod,b)%mod*qmo(qmo(s,i)*qmo(s+1,a-i)%mod,d)%mod;
33         if(i&1) ans=(ans-res+mod)%mod;else ans=(ans+res)%mod;
34     } return ans;
35 }
36
37 namespace WSN{
38     inline short main(){
39         n=read(); pre();
40         for(int i=1;i<=n;i++) a[i]=read(),m[i]=a[i];
41         for(int i=1;i<=n;i++) b[i]=read(),m[i+n]=b[i];
42         sort(a+1,a+n+1); sort(b+1,b+n+1);
43         if(a[n]!=b[n]) return puts("0"),0;
44         sort(m+1,m+2*n+1); has=unique(m+1,m+2*n+1)-m-1;
45         int pa=n+1,pb=n+1,na=n,nb=n;
46         for(int i=has;i;i--){
47             while(a[na-1]==m[i]&&na-1) --na;
48             while(b[nb-1]==m[i]&&nb-1) --nb;
49             ans=ans*calc(pa-na,pb-nb,n-pa+1,n-pb+1,m[i])%mod;
50             pa=na; pb=nb;
51         } write(ans);
52         return 0;
53     }
54 }
55 signed main(){return WSN::main();}

T3 seat

据说$dp$很玄学，不大会。。。。

只知道$skyh$大神倾情压行代码加注释。

$UPD 2021.9.9$

好了，差不多会了（只能说是一知半解）

代码里面的注释非常多了，直接看着那个理解就好了。。。

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 namespace AE86{
  4     inline int read(){
  5         int x=0,f=1;char ch=getchar();
  6         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
  7         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
  8     }inline void write(int x,char opt='\n'){
  9         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
 10         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
 11         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
 12 }using namespace AE86;
 13
 14 const int NN=1030;
 15 int n,mod,inv[NN],vis[NN];
 16 int cnt[NN];//记录对于距离为i的区间有几个，也就是 记录分出的log层，每一层区间的个数
 17 int pos[NN];//每个人对应的位置
 18 int odd[NN];//偶数长度大小的区间的个数,也是在这一层的人数
 19 int ans[NN][NN];//记录答案
 20 int f[NN][NN],g[NN][NN];
 21
 22 inline int qmo(int a,int b){int ans=1,c=mod; a%=c;while(b){if(b&1) ans=ans*a%c;b>>=1; a=a*a%c;} return ans;}
 23
 24 namespace WSN{
 25     inline short main(){
 26         n=read(); mod=read(); vis[0]=vis[n+1]=1;
 27         for(int i=1;i<=n;i++) inv[i]=qmo(i,mod-2);
 28         for(int i=1;i<=n;i++){
 29             int L=0,R=0,l=0,maxn=0;
 30             while(l<=n){//注意l表示区间左端点-1,r表示右端点+1
 31                 int r=l+1;
 32                 while(!vis[r])++r;
 33                 if(r-l>R-L) R=r,L=l;
 34                 l=r;
 35             }
 36             ++cnt[maxn=R-L>>1]; //maxn记录区间中的那个人与两端的人的距离
 37             if(R-L&1) ++odd[maxn];//R-L为奇数，表示区间长度为偶数
 38             pos[i]=L+maxn; vis[L+maxn]=1;//标记有了座位的人的位置
 39         }
 40         int sum=n;
 41         for(int i=1;i<=n;i++) if(cnt[i]){
 42             int l=sum-cnt[i]+1,r=sum;
 43             if(i==1)//叶子节点特殊处理，题解上说的
 44                 for(int j=l;j<=r;j++) for(int k=l;k<=r;k++)
 45                     ans[j][pos[k]]=inv[cnt[i]];
 46             else{
 47                 for(int j=0;j<=cnt[i];j++) for(int k=0;k<=odd[i];k++) f[j][k]=0;
 48                 f[0][odd[i]]=1;
 49                 int last=l+odd[i]-1;//默认前面的区间是偶区间的最后一个人
 50                 //就是最后一个在偶区间里面的人
 51                 for(int j=1;j<=cnt[i];j++){
 52                     int oddw=0,evew=0;
 53                     for(int k=0;k<=odd[i];k++) if(f[j-1][k]){
 54                         int mu=(cnt[i]-(j-1))+k,w=0;
 55                         if(k){//如果有偶数剩余
 56                             w=f[j-1][k]*k%mod*2%mod*inv[mu]%mod;//w辅助转移，k表示偶数的区间个数，所以转移位置都是2×k
 57                             (oddw+=w*inv[odd[i]*2])%=mod;
 58                             (f[j][k-1]+=w)%=mod;
 59                         }
 60                         if(cnt[i]-odd[i]){//如果有奇数剩余
 61                             w=f[j-1][k]*(mu-k*2+mod)%mod*inv[mu]%mod;//减去偶数转移点
 62                             (evew+=w*inv[(cnt[i]+odd[i])-odd[i]*2])%=mod;//注意总转移点个数为cnt[i]+odd[i]
 63                             (f[j][k]+=w)%=mod;//注意k不-1,因为转移的是奇数
 64                         }
 65                     }
 66                     for(int k=l;k<=last;k++) (ans[l+j-1][pos[k]]+=oddw)%=mod,(ans[l+j-1][pos[k]+1]+=oddw)%=mod;
 67                     //偶数可以选择的两个位置分别是pos[k],pos[k]+1,以此累加答案
 68                     for(int k=last+1;k<=r;k++) (ans[l+j-1][pos[k]]+=evew)%=mod;
 69                     //奇数同理
 70                 }
 71                 for(int j=l;j<=last;j++){
 72                     int L=pos[j]-i+1,R=pos[j]+i;//j这个人所在区间的左右端点
 73                     for(int k=L;k<=R;k++) if(pos[j]!=k)//枚举区间内每个位置
 74                         for(int u=r+1;u<=n;u++){
 75                             int s=(k<pos[j]?k+i+1:k-i);//找到等对称点
 76                             //关于等对称点，我们看一下下面我手玩的样例
 77                             /*
 78                                 |___|___|___|___|___|
 79                                 7   8   9   10  11  12
 80                                 这个样例的pos[j]为9，(因为不知道是哪个人，pos没有写下标)，距离i为3，
 81                                 L=7 ，R=12
 82                                 这样发现，如果j这个人选择在9,那么区间划分成7,8和10,11,12
 83                                 如果这个人在10,那么区间划分成7,8,9和11,12
 84                                 这样{
 85                                     7->11
 86                                     8->12
 87                                     10->7
 88                                     11->8
 89                                     12->9
 90                                 }
 91                                 按这样进行编码就会是以上的那样。
 92                              */
 93                             int w=ans[u][k]*inv[2]%mod;//后一个人在位置k的概率除以2
 94                             (g[u][k]+=w)%=mod; (g[u][s]+=w)%=mod; //然后把w均分到这两种等效的情况上
 95                             //此时会出现两个位置可供选择
 96                             //但无论选择哪一个,都会将区间划分成长度为n/2和n/2-1的两段。
 97                             //因此这两种选择具有对称性,我们只需要假定选择其中的一个,算出这种情况下之后的层的答案,即可对称地推出另一种情况下的答案。
 98                             //以上的均分找对称点就可以解决如上题解所说的问题
 99                         }
100                     for(int k=L;k<=R;k++) for(int u=r+1;u<=n;u++) ans[u][k]=g[u][k],g[u][k]=0;
101                 }
102             }
103             sum-=cnt[i];//减掉处理完的人数;
104         }
105         for(int i=1;i<=n;i++){
106             for(int j=1;j<=n;j++)
107                 write(ans[i][j],' ');
108             puts("");
109         }
110         return 0;
111     }
112 }
113 signed main(){return WSN::main();}

超级详细的注释代码