Solution Set -「LOCAL」冲刺省选 Round XXIV

\(\mathscr{Summary}\)

  名副其实的 trash round，希望以后没有了。

  A 题算好，确实一个比较关键的简化状态的点没想到，所以只拿了暴力（不考虑 \(\mathcal O(n^4)\) 能操过更多分的情况，明明 \(\mathcal O(n^4)\) 和 \(\mathcal O(2^n)\) 是一档的。）

  B 题签到，C 题倍增 + 分治 NTT 你开 \(10^6\) 我确实 ，要不是 \(10^5\) 分多我甚至懒得写。

\(\mathscr{Solution}\)

\(\mathscr{A}-\) Good

  给定 \(\{a_n\},\{w_n\}\)，每次可以在 \(\{a_n\}\) 中删去一个先升再降相邻差 \(1\) 的子串，删去长度为 \(l\) 的子串的收益为 \(w_l\)。求经过任意次操作获得的最大收益。

  \(n\le400\)。

---

  联系 \(n\) 的范围猜测是区间 DP，所以先莽一个 \(f(l,r)\)：把 \(a_{l..r}\) 删干净的最大收益（求出 \(f\) 之后可以再 DP 一下求答案）。注意“子串”成为“子序列”，能够划分子问题，所以自然想到转移时去讨论 \(a_l\) 被怎样的操作删除。

  这一点比较巧妙，也算是一个“删子串”转移的 trick：如果删除 \(a_l\) 时没有一起删除 \(a_r\)，那么 \(a_{l..r}\) 本身就能分成两段独立转移，所以我们只需要考虑 \(a_l\) 和 \(a_r\) 一起被删掉的操作。

  接下来就简单了。定义 \(g(l,r)\) 表示从 \(a_l\) 出发升序删子序列删到 \(a_r\) 所划分出的子问题 \(f\) 的最大和；\(h(l,r)\) 则为降序删子序列。那么

\[f(l,r)=\max_{i\in[l,r)}\{f(l,i)+f(i+1,r)\}+\max_{i\in[l,r]}\{g(l,i)+h(i,r)+w_{2a_i-a_l-a_r+1}\},\\
g(l,r)=\max_{i\in[l,r),a_i+1=a_r}\{g(l,i)+f(i+1,r-1)\},\\
h(l,r)=\max_{i\in(l,r],a_i+1=a_l}\{f(l+1,i-1)+h(i,r)\}.
\]

\(\mathcal O(n^3)\) 转移即可。

\(\mathscr{B}-\) Color

  给定含有 \(n\) 个点 \(m\) 条边的连通无向图，结点 \(u\) 有颜色 \(c_u\)。每次修改一个结点的颜色，修改后求出异色结点间的最短路。

  \(n\le2\times10^5\)，\(m\le3\times10^5\)，边权非负。

---

  显然最短路一定是一条边；显然只有 MST 上的边有用；显然可以 \(\mathcal O(q\log n)\) 在树上做。

\(\mathscr{C}-\) Music

  给定 \(\{v_n\}\)，求序列 \(S=\{s_n\}\) 的个数，使得 \(1\le s_i\le v_i\)，且 \(S\) 没有 border。

  \(n\le10^6\)，\(v_i\le v_{i+1}\)。

---

  注意 \(v_i\le v_{i+1}\) 这个限制告诉我们，对于 \(S\) 的任意一个 \(|S|/2\) 以内的前缀，我们可以让它成为 border。所以不难设计出基于此的暴力 DP，令 \(f(i)\) 表示仅考虑 \(s_{1..i}\) 的答案，\(p_i=\prod_{j=1}^iv_j\)，那么

\[f(i)=p_i-\sum_{j=1}^{i/2}\frac{f(j)}{p_j}\cdot p_{i-j}.
\]

  发现这是一个很像卷积的东西，但是它要求 \(p(x)\cdot q(x)\) 时，\(p\) 取出的 \(x\) 指数不小于 \(q\) 取出的 \(x\) 指数。从分治乘法的角度考虑，显然所有左端点不为 \(1\) 的区间无法内部转移，所以分治实质上是一个倍增。随便写写画画可以设计这样一个倍增方法：

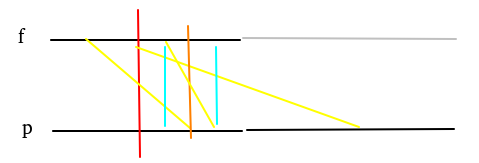
我们想要求 \(f\) 的灰色部分；红线是当前的中点，橙线是右半部分的中点。黄色连线可以直接卷，蓝色连线递归处理做上文提及的特殊卷积。特殊卷积的复杂度 \(T(n)=\mathcal O(n\log n)+2T(n/2)=\mathcal O(n\log^2n)\)，总复杂度 \(F(n)=T(n)+F(n/2)=\mathcal O(n\log^2n)\)。这个 \(10^6\) 带俩 \(\log\) 跑多项式？我的笔记本也是超神只用 \(0.7\text s\) 跑大样例，总之这就是正解，我也想问候出题人。