CodeForces - 983B XOR-pyramid（区间dp，异或）

XOR-pyramid

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

For an array bb of length mm we define the function ff as

f(b)={b[1]if m=1f(b[1]⊕b[2],b[2]⊕b[3],…,b[m−1]⊕b[m])otherwise,f(b)={b[1]if m=1f(b[1]⊕b[2],b[2]⊕b[3],…,b[m−1]⊕b[m])otherwise,

where ⊕⊕ is bitwise exclusive OR.

For example, f(1,2,4,8)=f(1⊕2,2⊕4,4⊕8)=f(3,6,12)=f(3⊕6,6⊕12)=f(5,10)=f(5⊕10)=f(15)=15f(1,2,4,8)=f(1⊕2,2⊕4,4⊕8)=f(3,6,12)=f(3⊕6,6⊕12)=f(5,10)=f(5⊕10)=f(15)=15

You are given an array aa and a few queries. Each query is represented as two integers ll and rr. The answer is the maximum value of ff on all continuous subsegments of the array al,al+1,…,aral,al+1,…,ar.

Input

The first line contains a single integer nn (1≤n≤50001≤n≤5000) — the length of aa.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai≤230−10≤ai≤230−1) — the elements of the array.

The third line contains a single integer qq (1≤q≤1000001≤q≤100000) — the number of queries.

Each of the next qq lines contains a query represented as two integers ll, rr (1≤l≤r≤n1≤l≤r≤n).

Output

Print qq lines — the answers for the queries.

Examples

input

Copy

3
8 4 1
2
2 3
1 2

output

Copy

5
12

input

Copy

6
1 2 4 8 16 32
4
1 6
2 5
3 4
1 2

output

Copy

60
30
12
3

Note

In first sample in both queries the maximum value of the function is reached on the subsegment that is equal to the whole segment.

In second sample, optimal segment for first query are [3,6][3,6], for second query — [2,5][2,5], for third — [3,4][3,4], for fourth — [1,2][1,2].

给n个数，询问q次，每次询问给出l,r.   [l,r]区间求异或最大值为多少。一开始没看清是最大值，还以为题目错了。

区间【1,6】和区间【2,5】比较一下就知道很多会重复，所以把它们记下来节省时间。

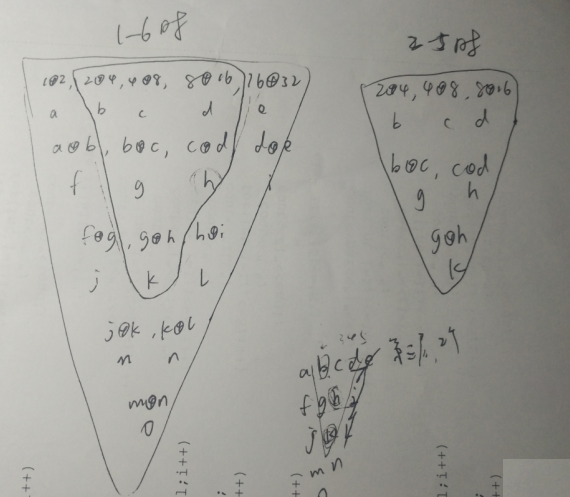
此题需要记忆化两次。区间动态规划。

我用b数组来存储所以异或的值，dp数来存储最大值。

拿第二个样例：

b数组这样得来：

b[1]这一排还是a数组

b[i][j]=b[i-1][j]^b[i-1][j+1];

dp数组这样的来：

dp[0]这一排还是a数组

dp[i][j]=max( dp[i-1][j], dp[i-1][j+1]，b[i][j] );

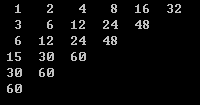  这是dp数组

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define maxn 110
#define maxm 10010
#define inf 0x3f3f3f
using namespace std;
int b[][];
int dp[][];
int a[];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
        dp[][i]=a[i];
    }
    for(int i=;i<=n-;i++)
    {
        b[][i]=a[i]^a[i+];
        dp[][i]=max(a[i],a[i+]);//第一排也是要比较得到dp[1][i]，否则第三个样例wa
        dp[][i]=max(b[][i],dp[][i]);
    }
    for(int i=;i<=n-;i++)
    {
        for(int j=;j<=n-i;j++)
        {
            b[i][j]=b[i-][j]^b[i-][j+];
        }
    }
    for(int i=;i<=n-;i++)
    {
        for(int j=;j<=n-i;j++)
        {
            dp[i][j]=max(dp[i-][j],dp[i-][j+]);
            dp[i][j]=max(dp[i][j],b[i][j]);
        }
    }
    for(int i=;i<=n-;i++)
    {
        for(int j=;j<=n-i;j++)
        {
            printf("%4d",dp[i][j]);
        }
        cout<<endl;
    }
    int q;
    scanf("%d",&q);
    while(q--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",dp[r-l][l]);
    }
    return ;
}