动态规划-背包问题 Knapsack

2018-03-15 13:11:12

背包问题（Knapsack problem）是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。

相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。

一、0/1背包问题

背包问题是个NPC问题，01背包可以通过动态规划算法在伪多项式时间内给出解。

0/1背包问题的特点是，每种物品仅仅有一件，且需要选择放或者不放。

在0/1背包问题中，物品i或者被装入背包，或者不被装入背包，设xi表示物品i装入背包的情况，则当xi=0时，表示物品i没有被装入背包，xi=1时，表示物品i被装入背包。根据问题的要求，有如下约束条件和目标函数：

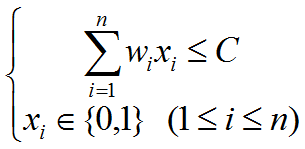
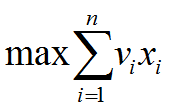
于是，问题归结为寻找一个满足约束条件式2.1，并使目标函数式2.2达到最大的解向量X=(x1, x2, …, xn)。

0/1背包问题可以看作是决策一个序列(x1, x2, …, xn)，对任一变量xi的决策是决定xi=1还是xi=0。在对xi-1决策后，已确定了(x1, …, xi-1)，在决策xi时，问题处于下列两种状态之一：
（1）背包容量不足以装入物品i，则xi=0，背包不增加价值；
（2）背包容量可以装入物品i，则xi=1，背包的价值增加了vi。
这两种情况下背包价值的最大者应该是对xi决策后的背包价值。令V(i, j)表示在前i(1≤i≤n)个物品中能够装入容量为j（1≤j≤C）的背包中的物品的最大值，则可以得到如下动态规划函数：

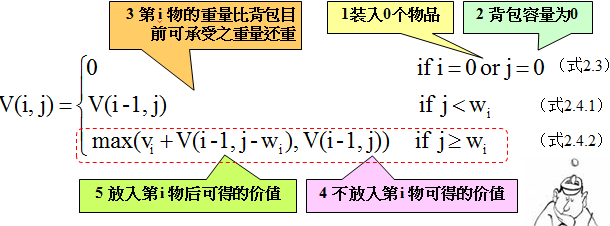
式2.3表明：把前面i个物品装入容量为0的背包和把0个物品装入容量为j的背包，得到的价值均为0。
式2.4的第一个式子表明：如果第i个物品的重量大于背包的容量，则装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价值是相同的，即物品i不能装入背包；第二个式子表明：如果第i个物品的重量小于背包的容量，则会有以下两种情况：
（1）如果把第i个物品装入背包，则背包中物品的价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi；
（2）如果第i个物品没有装入背包，则背包中物品的价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。显然，取二者中价值较大者作为把前i个物品装入容量为j的背包中的最优解。

举个例子：

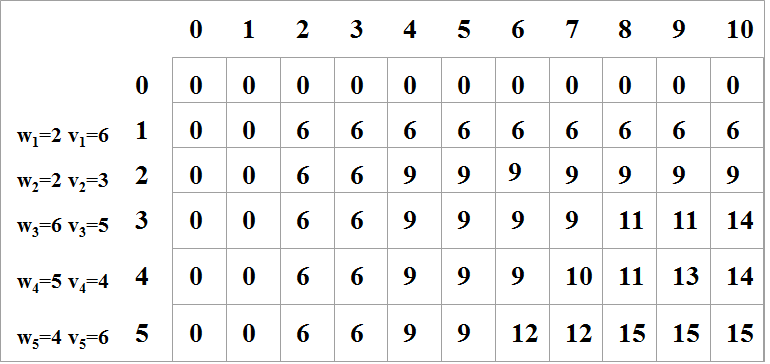
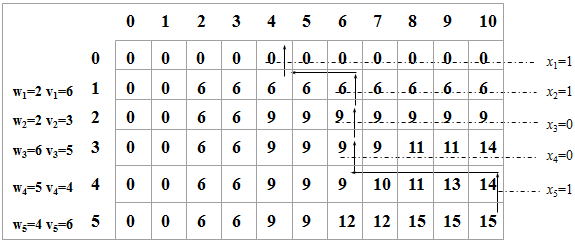
例如，有5个物品，其重量分别是{2, 2, 6, 5, 4}，价值分别为{6, 3, 5, 4, 6}，背包的容量为10。
根据动态规划函数，用一个(n+1)×(C+1)的二维表V，V[i][j]表示把前i个物品装入容量为j的背包中获得的最大价值。

第一阶段，只装入前1个物品，确定在各种情况下的背包能够得到的最大价值；
第二阶段，只装入前2个物品，确定在各种情况下的背包能够得到的最大价值；
依此类推，直到第n个阶段。最后，V(n,C)便是在容量为C的背包中装入n个物品
时取得的最大价值。

如何确定装入背包的具体物品？

从V(n,C)的值向前推，如果V(n,C)>V(n-1,C)，表明第n个物品被装入背包，前n-1个物品被装入容量为C-wn的背包中；否则，第n个物品没有被装入背包，前n-1个物品被装入容量为C的背包中。依此类推，直到确定第1个物品是否被装入背包中为止。由此，得到如下函数：

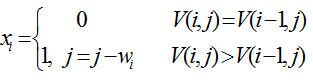
public class Knapsack {
    static int knapsack(int[] v, int[] w, int W) {
        int n = v.length;
        int[][] V = new int[n + 1][W + 1];
        int[] x = new int[n + 1];
        for (int i = 0; i < W + 1; i++) {
            V[0][i] = 0;
        }
        for (int i = 0; i < n + 1; i++) {
            V[i][0] = 0;
        }
 
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= W; j++) {
                if (j < w[i - 1]) V[i][j] = V[i - 1][j];
                else V[i][j] = Math.max(V[i - 1][j - w[i - 1]] + v[i - 1], V[i - 1][j]);
            }
        }
 
        int j = W;
        for (int i = n; i >= 1; i--) {
            if (V[i][j] == V[i - 1][j]) x[i] = 0;
            else {
                j -= w[i - 1];
                x[i] = 1;
            }
        }
 
        for (int i = 1; i <= n; i++) {
            System.out.println(x[i]);
        }
        return V[n][W];
    }
 
    public static void main(String[] args) {
        System.out.println(knapsack(new int[]{6, 3, 5, 4, 6}, new int[]{2, 2, 6, 5, 4}, 10));
    }
}

相关的优化处理：

时间复杂度已经无法进一步进行优化了，但是空间复杂度还是有优化余地的，通过递推式可以看到，每次下一行的值的产生仅仅依赖于上一行的前面两个值，因此，我们可以将二维数组优化成一维数组进行存储。

    static int polish(int[] v, int[] w, int W){
        int n = v.length;
        int[] m = new int[W + 1];
        m[0] = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = W; j >= w[i - 1]; j--) {
                m[j] = Math.max(m[j - w[i - 1]] + v[i - 1], m[j]);
            }
        }
        return m[W];
    }

另外，在初始化的时候，如果是题目没有要求必须得最终装满背包，则直接使用上述代码即可，如果题目中指出必须装满背包，则在初始化的时候，除了V[0][0] = 0外，其余的0件物品，j个重量，抑或j个重量，0件物品都是不满足装满背包的条件的，应该初始化为负无穷大。

二、完全背包问题

完全背包问题同样给出了n件物品的重量和价值，并且给出了背包的大小W，但是和0/1背包不同的是，在完全背包问题中，每件物品可以选1，2，3...直到背包放不下为止。

完全背包是0/1背包问题的一个扩展，也同样是一个非常经典的问题。

运用类比的思想，我们可以将完全背包转化成0/1背包，具体的转化可以有下面两种方式：

1、将每件物品看成W/w[i]件，价值不变；

2、将每件物品看成v[i]*2^k，重量为w[i]*2^k，想法就是利用二进制的角度看问题，任何多种选择都可以通过这些二进制数相加得到，这种方法的分解个数显然要小很多，非常聪明。

如果从递推式的角度来解决问题，可以得到一个非常好的解答：

V[i][j] = max{V[i - 1][j]， V[i][j - w[i]] + v[i]}

对于每一个V[i][j]都可以看成要么不选择第i件，要么选择第i件且可以多选，那么就可以很容易的得到上述的递推式。

下面使用一维数组进行实现，你会发现除了内层的顺序变了，其他的都没有改变。

    static int polish(int[] v, int[] w, int W){
        int n = v.length;
        int[] m = new int[W + 1];
        m[0] = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = w[i - 1]; j <= W; j--) {
                m[j] = Math.max(m[j - w[i - 1]] + v[i - 1], m[j]);
            }
        }
        return m[W];
    }