LCA最近公共祖先（Tarjan离线算法）

这篇博客对Tarjan算法的原理和过程模拟的很详细。

转载大佬的博客https://www.cnblogs.com/JVxie/p/4854719.html

第二次更新，之前转载的博客虽然胜在详细，但其实还是对递归，集合划分，查找还是有些抽象，刚刚恰好看了千千大佬的一篇博客，他在讲解Tarjan算法的时候，用了不同的颜色来区别不同的集合，我觉得这一点非常的好，现在我自己也对Tarjan算法有了一些理解，使用DFS的目的首先是递归中‘递’过程，不断深搜到底；接着回溯使用并查集划分集合，要找LCA的会被放入一个集合中，其LCA就是这个集合的祖先。

转载千千大佬的个人博客加载在本篇博文之后https://www.dreamwings.cn/lca/4874.html

首先什么是最近公共祖先：

在一棵没有环的树上，每个节点肯定有其父亲节点和祖先节点，而最近公共祖先，就是两个节点在这棵树上深度最大的公共的祖先节点。换

句话说，就是两个点在这棵树上距离最近的公共祖先节点。所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。

有人可能会问：那他本身或者其父亲节点是否可以作为祖先节点呢？

答案是肯定的，很简单，按照人的亲戚观念来说，你的父亲也是你的祖先，而LCA还可以将自己视为祖先节点。

举个例子吧，如下图所示４和５的最近公共祖先是２，５和３的最近公共祖先是１，２和１的最近公共祖先是１。　

这就是最近公共祖先的基本概念了，那么我们该如何去求这个最近公共祖先呢？

通常初学者都会想到最简单粗暴的一个办法：对于每个询问，遍历所有的点，时间复杂度为O(n*q)，很明显，n和q一般不会很小。

常用的求LCA的算法有：Tarjan/DFS+ST/倍增

后两个算法都是在线算法，也很相似，时间复杂度在O(logn)~O(nlogn)之间，我个人认为较难理解。

有的题目是可以用线段树来做的，但是其代码量很大，时间复杂度也偏高，在O(n)~O(nlogn)之间，优点在于也是简单粗暴。

这篇博客主要是要介绍一下Tarjan算法(其实是我不会在线...)。

什么是Tarjan(离线)算法呢？顾名思义，就是在一次遍历中把所有询问一次性解决，所以其时间复杂度是O(n+q)。

Tarjan算法的优点在于相对稳定，时间复杂度也比较居中，也很容易理解。

下面详细介绍一下Tarjan算法的基本思路：

1.任选一个点为根节点，从根节点开始。

2.遍历该点u所有子节点v，并标记这些子节点v已被访问过。

3.若是v还有子节点，返回2，否则下一步。

4.合并v到u上。

5.寻找与当前点u有询问关系的点v。

6.若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

遍历的话需要用到dfs来遍历(我相信来看的人都懂吧...)，至于合并，最优化的方式就是利用并查集来合并两个节点。

下面上伪代码：

　　 1 Tarjan(u)//marge和find为并查集合并函数和查找函数
 　　2 {
 　　3     for each(u,v)    //访问所有u子节点v
 　　4     {
　　 5         Tarjan(v);        //继续往下遍历
　　 6         marge(u,v);    //合并v到u上
　　 7         标记v被访问过;
　　 8     }
　　 9     for each(u,e)    //访问所有和u有询问关系的e
　　10     {
　　11         如果e被访问过;
　　12         u,e的最近公共祖先为find(e);
　　13     }
　　14 }

个人感觉这样还是有很多人不太理解，所以我打算模拟一遍给大家看。

建议拿着纸和笔跟着我的描述一起模拟！！

假设我们有一组数据 9个节点 8条边 联通情况如下：

1--2，1--3，2--4，2--5，3--6，5--7，5--8，7--9 即下图所示的树

设我们要查找最近公共祖先的点为9--8，4--6，7--5，5--3；

设f[]数组为并查集的父亲节点数组，初始化f[i]=i，vis[]数组为是否访问过的数组，初始为0;　

下面开始模拟过程：

取1为根节点，往下搜索发现有两个儿子2和3；

先搜2，发现2有两个儿子4和5，先搜索4，发现4没有子节点，则寻找与其有关系的点；

发现6与4有关系，但是vis[6]=0，即6还没被搜过，所以不操作；

发现没有和4有询问关系的点了，返回此前一次搜索，更新vis[4]=1；

　　　　

表示4已经被搜完，更新f[4]=2，继续搜5，发现5有两个儿子7和8;

先搜7，发现7有一个子节点9，搜索9，发现没有子节点，寻找与其有关系的点；

发现8和9有关系，但是vis[8]=0,即8没被搜到过，所以不操作；

发现没有和9有询问关系的点了，返回此前一次搜索，更新vis[9]=1；

表示9已经被搜完，更新f[9]=7，发现7没有没被搜过的子节点了，寻找与其有关系的点；

发现5和7有关系，但是vis[5]=0，所以不操作；

发现没有和7有关系的点了，返回此前一次搜索，更新vis[7]=1；

　　　　

表示7已经被搜完，更新f[7]=5，继续搜8，发现8没有子节点，则寻找与其有关系的点；

发现9与8有关系，此时vis[9]=1，则他们的最近公共祖先为find(9)=5；

(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;)

发现没有与8有关系的点了，返回此前一次搜索，更新vis[8]=1；

表示8已经被搜完，更新f[8]=5，发现5没有没搜过的子节点了，寻找与其有关系的点；

　　　　

发现7和5有关系，此时vis[7]=1，所以他们的最近公共祖先为find(7)=5；

(find(7)的顺序为f[7]=5-->f[5]=5 return 5;)

又发现5和3有关系，但是vis[3]=0，所以不操作，此时5的子节点全部搜完了；

返回此前一次搜索，更新vis[5]=1，表示5已经被搜完，更新f[5]=2；

发现2没有未被搜完的子节点，寻找与其有关系的点；

又发现没有和2有关系的点，则此前一次搜索，更新vis[2]=1；

　　　　

表示2已经被搜完，更新f[2]=1，继续搜3，发现3有一个子节点6；

搜索6，发现6没有子节点，则寻找与6有关系的点，发现4和6有关系；

此时vis[4]=1，所以它们的最近公共祖先为find(4)=1;

(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)

发现没有与6有关系的点了，返回此前一次搜索，更新vis[6]=1，表示6已经被搜完了；

　　　　

更新f[6]=3，发现3没有没被搜过的子节点了，则寻找与3有关系的点；

发现5和3有关系，此时vis[5]=1，则它们的最近公共祖先为find(5)=1；

(find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)

发现没有和3有关系的点了，返回此前一次搜索，更新vis[3]=1；

　　　　

更新f[3]=1，发现1没有被搜过的子节点也没有有关系的点，此时可以退出整个dfs了。

经过这次dfs我们得出了所有的答案，有没有觉得很神奇呢？是否对Tarjan算法有更深层次的理解了呢？

我们假设在如下树中模拟 Tarjan 过程（节点数量少一点可以画更少的图o(￣▽￣)o）

存在查询： LCA(T,3,4)、LCA(T,4,6)、LCA(T,2,1) 。

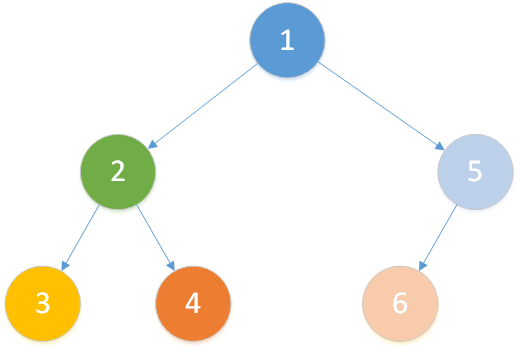
注意：每个节点的颜色代表它当前属于哪一个集合，橙色线条为搜索路径，黑色线条为合并路径。

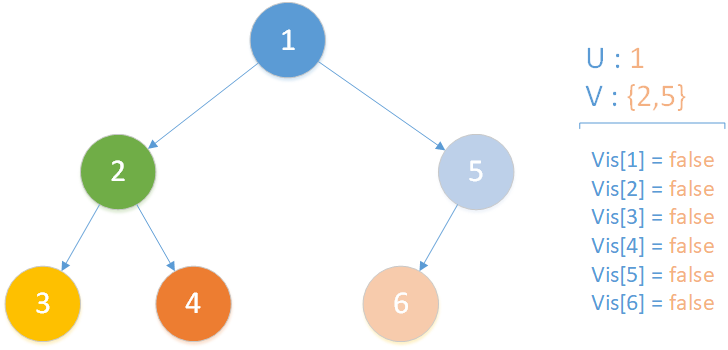
当前所在位置为 u = 1 ，未遍历孩子集合 v = {2,5} ，向下遍历。

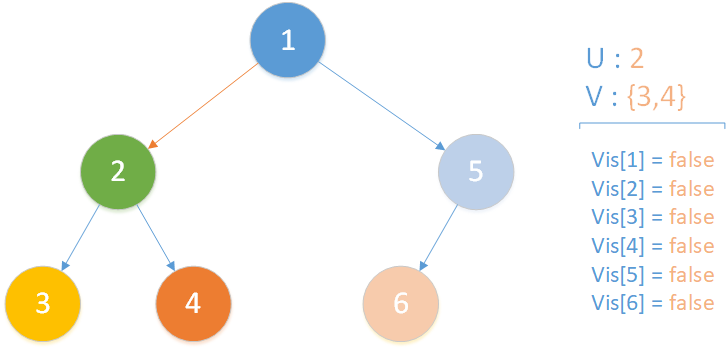
当前所在位置为 u = 2 ，未遍历孩子集合 v = {3,4} ，向下遍历。

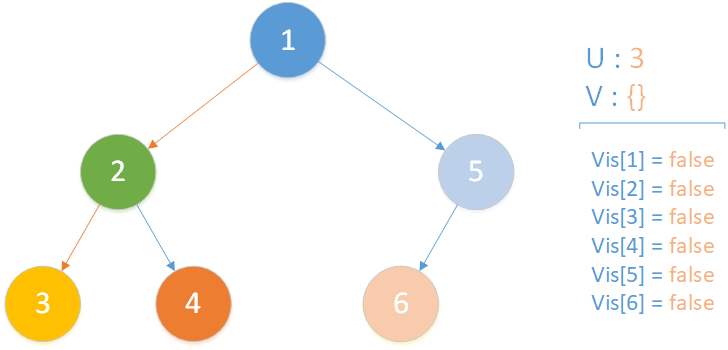
当前所在位置为 u = 3 ，未遍历孩子集合 v = {} ，递归到达最底层，遍历所有相关查询发现存在 LCA(T,3,4) ，但是节点 4 此时标记未访问，因此什么也不做，该层递归结束。

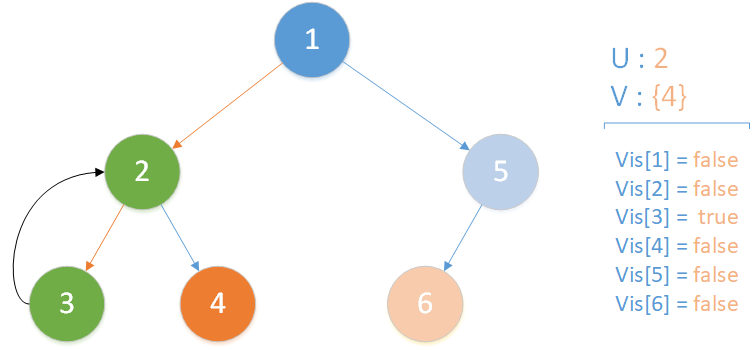
递归返回，当前所在位置 u = 2 ，合并节点 3 到 u 所在集合，标记 vis[3] = true ，此时未遍历孩子集合 v = {4} ，向下遍历。

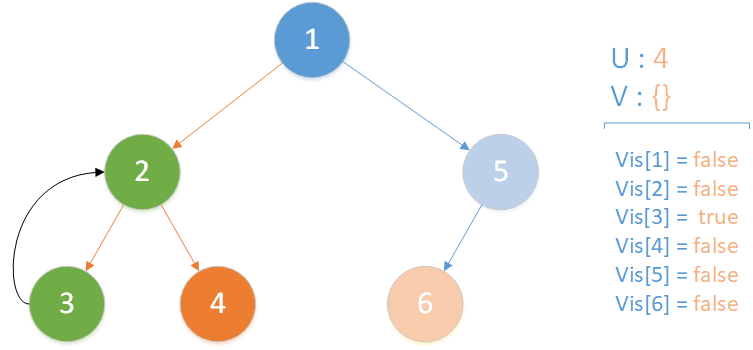
当前所在位置 u = 4 ，未遍历孩子集合 v = {} ，遍历所有相关查询发现存在 LCA(T,3,4) ，且 vis[3] = true ，此时得到该查询的解为节点 3 所在集合的首领，即 LCA(T,3,4) = 2 ；又发现存在相关查询 LCA(T,4,6) ，但是节点 6 此时标记未访问，因此什么也不做。该层递归结束。

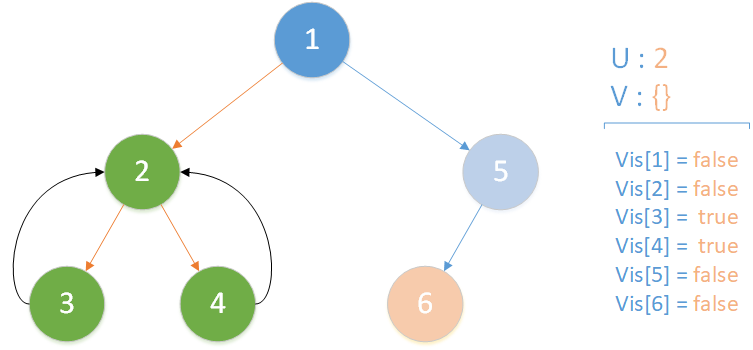
递归返回，当前所在位置 u = 2 ，合并节点 4 到 u 所在集合，标记 vis[4] = true ，未遍历孩子集合 v = {} ，遍历相关查询发现存在 LCA(T,2,1) ，但是节点 1 此时标记未访问，因此什么也不做，该层递归结束。

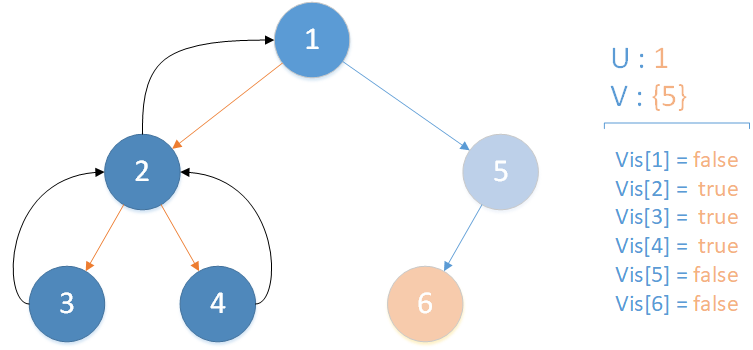
递归返回，当前所在位置 u = 1 ，合并节点 2 到 u 所在集合，标记 vis[2] = true ，未遍历孩子集合 v = {5} ，继续向下遍历。

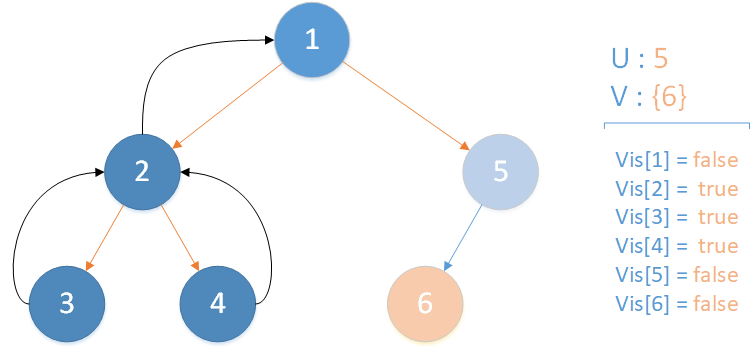
当前所在位置 u = 5 ，未遍历孩子集合 v = {6} ，继续向下遍历。

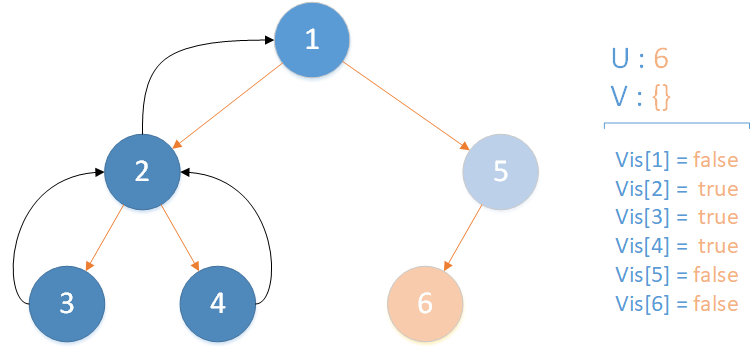
当前所在位置 u = 6 ，未遍历孩子集合 v = {} ，遍历相关查询发现存在 LCA(T,4,6) ，且 vis[4] = true ，因此得到该查询的解为节点 4 所在集合的首领，即 LCA(T,4,6) = 1 ，该层递归结束。

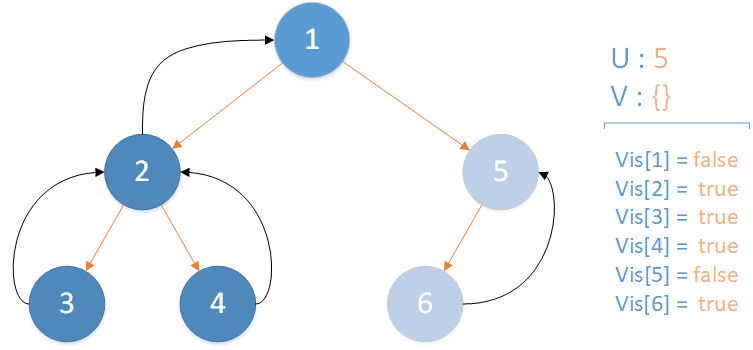
递归返回，当前所在位置 u = 5 ，合并节点 6 到 u 所在集合，并标记 vis[6] = true ，未遍历孩子集合 v = {} ，无相关查询因此该层递归结束。

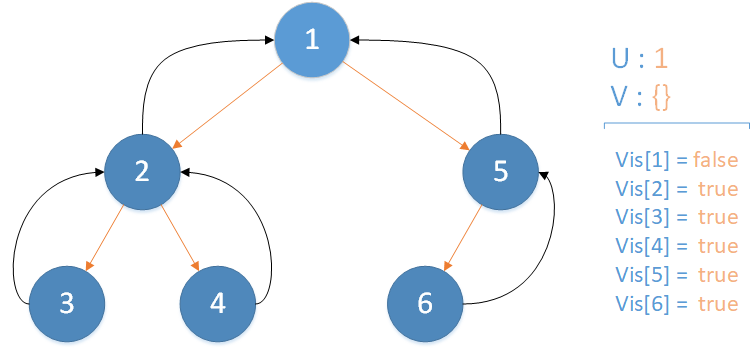
递归返回，当前所在位置 u = 1 ，合并节点 5 到 u 所在集合，并标记 vis[5] = true ，未遍历孩子集合 v = {} ，遍历相关查询发现存在 LCA(T,2,1) ，此时该查询的解便是节点 2 所在集合的首领，即 LCA(T,2,1) = 1 ，递归结束。

至此整个 Tarjan 算法便结束啦~

PS：不要在意最终根节点的颜色和其他节点颜色有一点点小小差距，可能是千千在染色的时候没仔细看，总之就这样咯~

PPS：所谓的首领就是、就是首领啦~