高斯分布（Gaussian Distribution）的概率密度函数（probability density function）

高斯分布（Gaussian Distribution）的概率密度函数（probability density function）

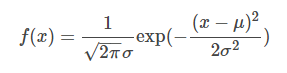
对应于numpy中：

numpy.random.normal(loc=0.0, scale=1.0, size=None)

参数的意义为：

loc：float
此概率分布的均值（对应着整个分布的中心centre）
scale：float
此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）
size：int or tuple of ints
输出的shape，默认为None，只输出一个值

我们更经常会用到的np.random.randn(size)所谓标准正态分布（μ=0,σ=1μ=0,σ=1），对应于np.random.normal(loc=0, scale=1, size)。

新建test.py文件

import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'  #忽略烦人的警告
import numpy;

y=numpy.random.normal(loc=0.0, scale=1.0, size=None)
print(y)

$ python test.py
-0.19073908191320865
(tensorflow)

$ python test.py
0.39479165603679667
(tensorflow)