《FFT家族—从不会到崩溃(坑)》读blog笔记

免责声明

原文地址https://blog.csdn.net/linjiayang2016/article/details/80341958，作者linjiayang2016.\text{linjiayang2016}.linjiayang2016.

本文是对原文的微薄补充，目的是为了更好地读懂原文。

正弦sin⁡\sinsin, 余弦cos⁡\coscos

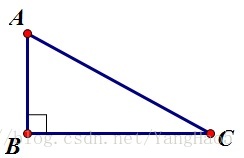
$RT.\ 在在在Rt△ABC中，中，中，∠B=90°$，则有

sin⁡ A=BCAC\sin\ A=\frac{BC}{AC}sin A=ACBC​

cos⁡ A=ABAC\cos\ A=\frac{AB}{AC}cos A=ACAB​

快速傅里叶变换过程

以用FFTFFTFFT解决多项式乘法的问题为例。

$1.\ 读入多项式读入多项式读入多项式a,b$；

$2.\ 对对对a,b$分别做傅里叶变换；

3. a∗=b3.\ a*=b3. a∗=b；

$4.\ 对对对a数组做逆变换并除以长度数组做逆变换并除以长度数组做逆变换并除以长度n$.

## 关于单位根的补充说明
$\ \ \ \ w^k_n*w^1_n$
$=(\cos\ k*\frac{2\pi}{n}+\sin\ k*\frac{2\pi}{n}\ i)\ *\ (\cos\ \frac{2\pi}{n}+\sin\ \frac{2\pi}{n}\ i)$
$=\cos\ k*\frac{2\pi}{n}\ *\ \cos\ \frac{2\pi}{n}\ +\ \sin\ k*\frac{2\pi}{n}\ i\ *\ \cos\ \frac{2\pi}{n}$
$\quad+\ \cos\ k*\frac{2\pi}{n}\ *\ \sin\ \frac{2\pi}{n}\ i\ +\ \sin\ k*\frac{2\pi}{n}\ i\ *\ \sin\ \frac{2\pi}{n}\ i$
$=\cos\ ((k+1)*\frac{2\pi}{n})\ +\ \sin\ ((k+1)*\frac{2\pi}{n})$
$=w^{k+1}_n.$


## 两角和公式
$\sin\ (A+B)=\sin\ A·\cos\ B+\cos\ A·\sin\ B$
$\cos\ (A+B)=\cos\ A·\cos B-\sin\ A·\sin\ B$


## 快速傅里叶逆变换
原文中的$y$指的是上文的$a$，原文中的$a$指答案数组.


对于$c_i=\sum\limits^{n-1}_{j=0}a_j(\sum\limits^{n-1}_{i=0}(w^{j-k}_n)^i)$$\ \ \ (k$是常数$)$，
$1.\ $当$j-k=0$时，$w^{j-k}_n=1+0i$，$\therefore \sum\limits^{n-1}_{i=0}(w^{j-k}_n)^i=n$；
$2.\ $当$j-k≠0$时，原文已阐述详尽，在此不做赘述.


## 线性求翻转序列
对于已知的翻转序列$r_i$，我们在它前面加上$1$或$0$，就得到了$r_{2i+1}$和$r_{2i+2}.$
举例. $\because r_6=11_{(2)}$，
$\therefore r_{13}=$ `0`$11_{(2)}.\ \ $(在$r_6$前补`0`)
$\quad r_{14}=$ `1`$11_{(2)}.\ \ $(在$r_6$前补`1`)