落谷P3941 入阵曲

题目背景

pdf题面和大样例链接：http://pan.baidu.com/s/1cawM7c 密码：xgxv

丹青千秋酿，一醉解愁肠。

无悔少年枉，只愿壮志狂。

题目描述

小 F 很喜欢数学，但是到了高中以后数学总是考不好。

有一天，他在数学课上发起了呆；他想起了过去的一年。一年前，当他初识算法竞赛的时候，觉得整个世界都焕然一新。这世界上怎么会有这么多奇妙的东西？曾经自己觉得难以解决的问题，被一个又一个算法轻松解决。

小 F 当时暗自觉得，与自己的幼稚相比起来，还有好多要学习的呢。

一年过去了，想想都还有点恍惚。

他至今还能记得，某天晚上听着入阵曲，激动地睡不着觉，写题写到鸡鸣时分都兴奋不已。也许，这就是热血吧。

也就是在那个时候，小 F 学会了矩阵乘法。让两个矩阵乘几次就能算出斐波那契数列的第 10^{100}10100 项，真是奇妙无比呢。

不过，小 F 现在可不想手算矩阵乘法——他觉得好麻烦。取而代之的，是一个简单的小问题。他写写画画，画出了一个 n \times mn×m 的矩阵，每个格子里都有一个不超过 kk 的正整数。

小 F 想问问你，这个矩阵里有多少个不同的子矩形中的数字之和是 kk 的倍数？如果把一个子矩形用它的左上角和右下角描述为 (x_1,y_1,x_2,y_2)(x1,y1,x2,y2)，其中x_1 \le x_2,y_1 \le y_2x1≤x2,y1≤y2；那么，我们认为两个子矩形是不同的，当且仅当他们以 (x_1,y_1,x_2,y_2)(x1,y1,x2,y2) 表示时不同；也就是说，只要两个矩形以 (x_1,y_1,x_2,y_2)(x1,y1,x2,y2) 表示时相同，就认为这两个矩形是同一个矩形，你应该在你的答案里只算一次。

输入输出格式

输入格式：

从标准输入中读入数据。

输入第一行，包含三个正整数 n,m,kn,m,k。

输入接下来 nn 行，每行包含 mm 个正整数，第 ii 行第 jj 列表示矩阵中第 ii 行第 jj 列中所填的正整数 a_{i,j}ai,j。

输出格式：

输出到标准输出中。

输入一行一个非负整数，表示你的答案。

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

【样例 1 说明】

这些矩形是符合要求的： (1, 1, 1, 3)，(1, 1, 2, 2)，(1, 2, 1, 2)，(1, 2, 2, 3)，(2, 1, 2, 1)，(2, 3, 2, 3)。

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解决一部分测试数据。

每个测试点的数据规模及特点如下表：

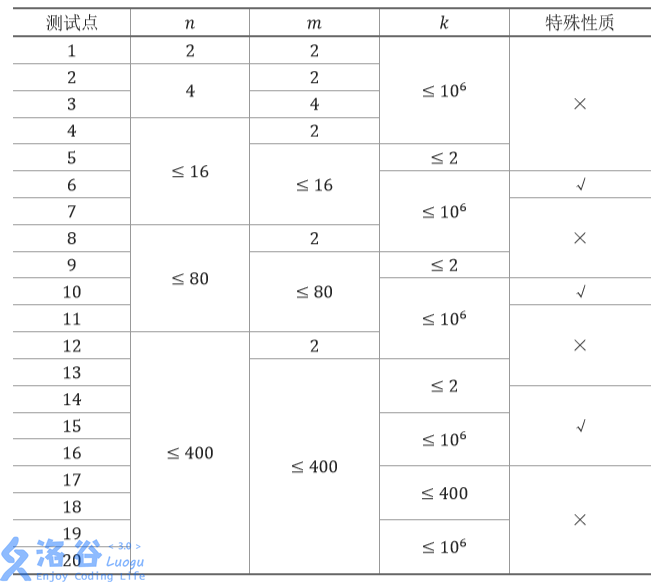
特殊性质：保证所有 a_{i,j}ai,j 均相同。

题解：

　　这个题目我们先考虑套路一下，记一下每一列的前缀合，然后枚举两行，把两行之间的数字压缩成一个数，这样就变成了一个序列问题，对答案有贡献的区间只有满足(sum[r]-sum[l-1])%k==0，即sum[r]%k==sum[l-1]%k，所以我们开一个sum的桶，每次查询和sum[r]%k相同的右端点个数就可以了。

题外话：

　　很久没有发博客了，因为都在做学校内部的题目，不方便发出来，真是，自己回来看博客的时候，发现虽然自己没动，但很多东西都变了。

代码：

#include <cstdio>

#include <iostream>

#include <algorithm>

#include <cstring>

#include <cmath>

#include <iostream>

#define RG register

#define ll long long

#define MAXN 410

using namespace std;

ll sum[MAXN][MAXN],a[MAXN][MAXN],tong[],sum2[MAXN],ans;

int n,m,k;

inline void work(int l,int r){

  for(RG int i=;i<=m;i++){

    ll now=sum[i][r]-sum[i][l-];

    sum2[i]=(sum2[i-]+now)%k;

    tong[sum2[i-]]++;

    ans+=tong[sum2[i]];

  }

  for(RG int i=;i<=m-;i++){

    tong[sum2[i]]--;

    sum2[i]=;

  }

}

int main()

{

  scanf("%d%d%d",&n,&m,&k);

  for(int i=;i<=n;i++){

    for(int j=;j<=m;j++) scanf("%lld",&a[i][j]);

  }

  for(RG int j=;j<=m;j++){

    for(RG int i=;i<=n;i++){

      sum[j][i]=sum[j][i-]+a[i][j];

    }

  }

  for(RG int l=;l<=n;l++){

    for(RG int r=l;r<=n;r++){

      work(l,r);

    }

  }

  printf("%lld",ans);

  return ;

}