玩透二叉树(Binary-Tree)及前序（先序）、中序、后序【递归和非递归】遍历

---

基础预热：

结点的度（Degree）：结点的子树个数；
树的度：树的所有结点中最大的度数；
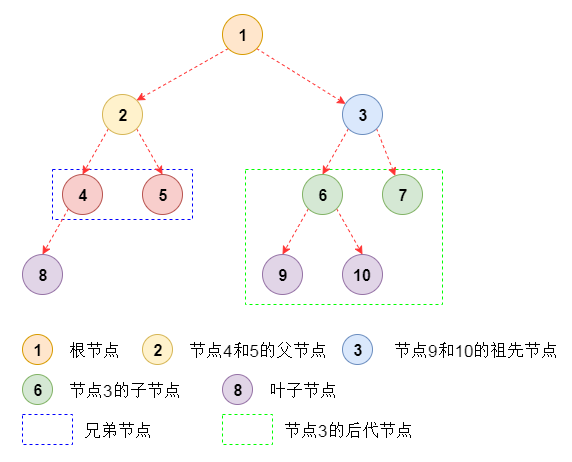
叶结点（Leaf）：度为0的结点；
父结点（Parent）：有子树的结点是其子树的根节点的父结点；
子结点/孩子结点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；
兄弟结点（Sibling）：具有同一个父结点的各结点彼此是兄弟结点；
路径和路径长度：从结点n1到nk的路径为一个结点序列n1，n2，…，nk。ni是ni+1的父结点。路径所包含边的个数为路径的长度；
祖先结点（Ancestor）：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点；
子孙结点（Descendant）：某一结点的子树中的所有结点是这个结点的子孙；
结点的层次（Level）：规定根结点在1层，其他任一结点的层数是其父结点的层数加1；
树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度；

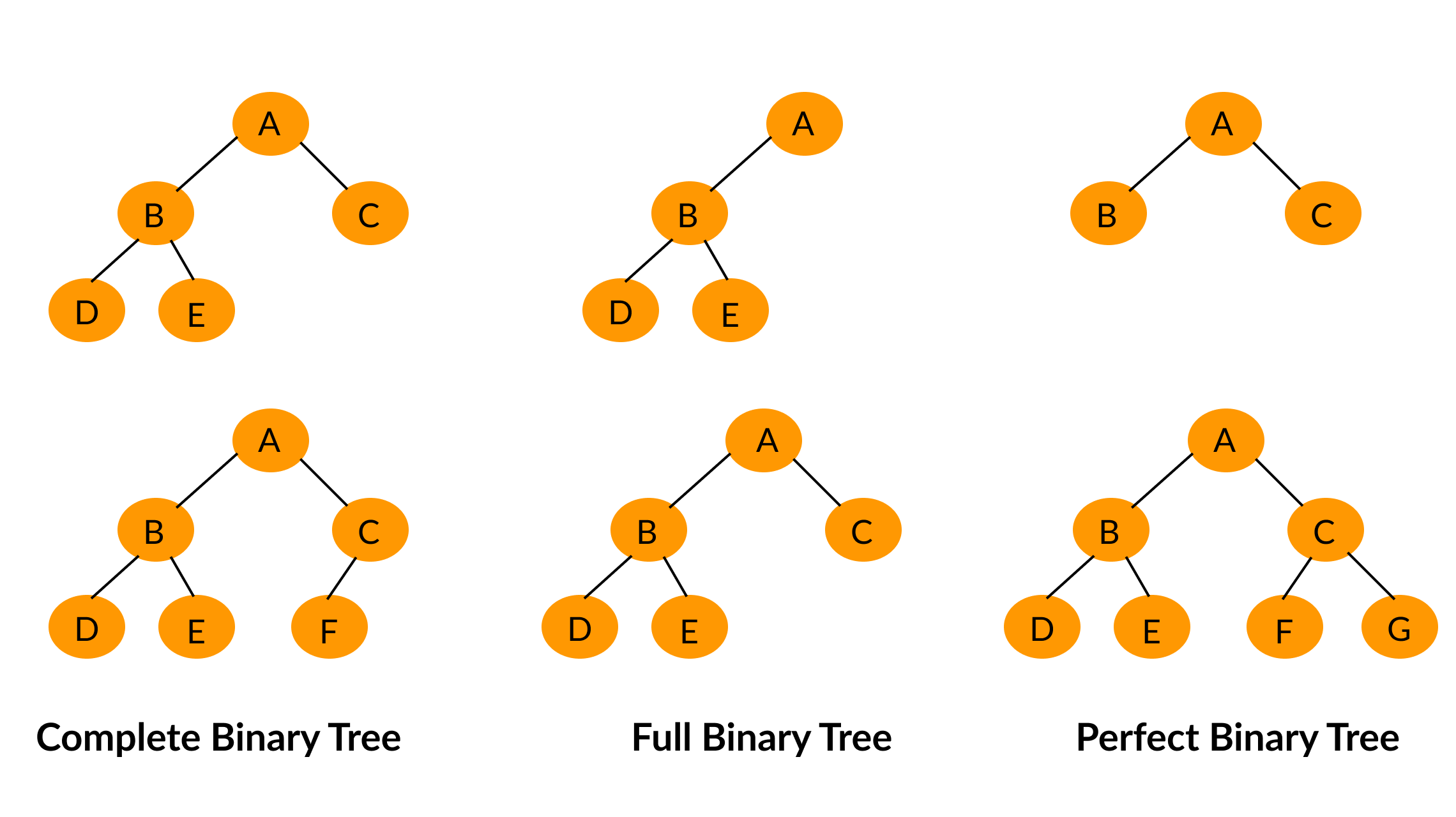
满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树。

完全二叉树

一棵二叉树至多只有最下面的一层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，则此二叉树成为完全二叉树。

平衡二叉树

它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

前序、中序、后序

首先给出二叉树节点类：

树节点：

class TreeNode {
    int val;
    //左子树
    TreeNode left;
    //右子树
    TreeNode right;
    //构造方法
    TreeNode(int x) {
        val = x;
    }
}

---

无论是哪种遍历方法，考查节点的顺序都是一样的(思考做试卷的时候，人工遍历考查顺序)。只不过有时候考查了节点，将其暂存，需要之后的过程中输出。

 

图2：先序、中序、后序遍历节点考查顺序

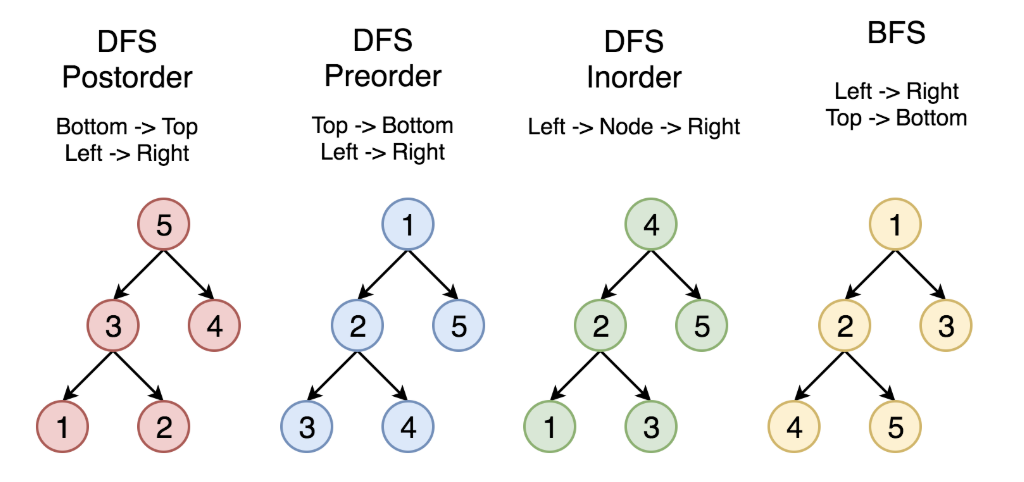
如图1所示，三种遍历方法(人工)得到的结果分别是：

先序：1 2 4 6 7 8 3 5
中序：4 7 6 8 2 1 3 5
后序：7 8 6 4 2 5 3 1

三种遍历方法的考查顺序一致，得到的结果却不一样，原因在于：

先序：考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右)

中序：考察到一个节点后，将其暂存，遍历完左子树后，再输出该节点的值，然后遍历右子树。(左根右)

后序：考察到一个节点后，将其暂存，遍历完左右子树后，再输出该节点的值。(左右根)

---

先序遍历

递归先序遍历

递归先序遍历很容易理解，先输出节点的值，再递归遍历左右子树。中序和后序的递归类似，改变根节点输出位置即可。

// 递归先序遍历
public static void recursionPreorderTraversal(TreeNode root) {
    if (root != null) {
        System.out.print(root.val + " ");
        recursionPreorderTraversal(root.left);
        recursionPreorderTraversal(root.right);
    }
}

非递归先序遍历

因为要在遍历完节点的左子树后接着遍历节点的右子树，为了能找到该节点，需要使用栈来进行暂存。中序和后序也都涉及到回溯，所以都需要用到栈。

 

图2：非递归先序遍历

遍历过程参考注释

// 非递归先序遍历
public static void preorderTraversal(TreeNode root) {
    // 用来暂存节点的栈
    Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
    // 新建一个游标节点为根节点
    TreeNode node = root;
    // 当遍历到最后一个节点的时候，无论它的左右子树都为空，并且栈也为空
    // 所以，只要不同时满足这两点，都需要进入循环
    while (node != null || !treeNodeStack.isEmpty()) {
        // 若当前考查节点非空，则输出该节点的值
        // 由考查顺序得知，需要一直往左走
        while (node != null) {
            System.out.print(node.val + " ");
            // 为了之后能找到该节点的右子树，暂存该节点
            treeNodeStack.push(node);
            node = node.left;
        }
        // 一直到左子树为空，则开始考虑右子树
        // 如果栈已空，就不需要再考虑
        // 弹出栈顶元素，将游标等于该节点的右子树
        if (!treeNodeStack.isEmpty()) {
            node = treeNodeStack.pop();
            node = node.right;
        }
    }
}

先序遍历结果：

递归先序遍历： 1 2 4 6 7 8 3 5
非递归先序遍历：1 2 4 6 7 8 3 5

---

中序遍历

递归中序遍历

过程和递归先序遍历类似

// 递归中序遍历
public static void recursionMiddleorderTraversal(TreeNode root) {
    if (root != null) {
        recursionMiddleorderTraversal(root.left);
        System.out.print(root.val + " ");
        recursionMiddleorderTraversal(root.right);
    }
}

非递归中序遍历

和非递归先序遍历类似，唯一区别是考查到当前节点时，并不直接输出该节点。

而是当考查节点为空时，从栈中弹出的时候再进行输出(永远先考虑左子树，直到左子树为空才访问根节点)。

// 非递归中序遍历
public static void middleorderTraversal(TreeNode root) {
    Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
    TreeNode node = root;
    while (node != null || !treeNodeStack.isEmpty()) {
        while (node != null) {
            treeNodeStack.push(node);
            node = node.left;
        }
        if (!treeNodeStack.isEmpty()) {
            node = treeNodeStack.pop();
            System.out.print(node.val + " ");
            node = node.right;
        }
    }
}

中序遍历结果

递归中序遍历： 4 7 6 8 2 1 3 5
非递归中序遍历：4 7 6 8 2 1 3 5

---

后序遍历

递归后序遍历

过程和递归先序遍历类似

// 递归后序遍历
public static void recursionPostorderTraversal(TreeNode root) {
    if (root != null) {
        recursionPostorderTraversal(root.left);
        recursionPostorderTraversal(root.right);
        System.out.print(root.val + " ");
    }
}

非递归后序遍历

后续遍历和先序、中序遍历不太一样。

后序遍历在决定是否可以输出当前节点的值的时候，需要考虑其左右子树是否都已经遍历完成。

所以需要设置一个lastVisit游标。

若lastVisit等于当前考查节点的右子树，表示该节点的左右子树都已经遍历完成，则可以输出当前节点。

并把lastVisit节点设置成当前节点，将当前游标节点node设置为空，下一轮就可以访问栈顶元素。

否者，需要接着考虑右子树，node = node.right。

以下考虑后序遍历中的三种情况：

 

图3：后序，右子树不为空，node = node.right

如图3所示，从节点1开始考查直到节点4的左子树为空。

注：此时的游标节点node = 4.left == null。

此时需要从栈中查看 Peek()栈顶元素。

发现节点4的右子树非空，需要接着考查右子树，4不能输出，node = node.right。

 

图4：后序，左右子树都为空，直接输出

如图4所示，考查到节点7(7.left == null，7是从栈中弹出)，其左右子树都为空，可以直接输出7。

此时需要把lastVisit设置成节点7，并把游标节点node设置成null，下一轮循环的时候会考查栈中的节点6。

 

图5：后序，右子树 = lastVisit，直接输出

如图5所示，考查完节点8之后(lastVisit == 节点8)，将游标节点node赋值为栈顶元素6，节点6的右子树正好等于节点8。表示节点6的左右子树都已经遍历完成，直接输出6。

此时，可以将节点直接从栈中弹出Pop()，之前用的只是Peek()。

将游标节点node设置成null。

// 非递归后序遍历
public static void postorderTraversal(TreeNode root) {
    Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
    TreeNode node = root;
    TreeNode lastVisit = root;
    while (node != null || !treeNodeStack.isEmpty()) {
        while (node != null) {
            treeNodeStack.push(node);
            node = node.left;
        }
        //查看当前栈顶元素
        node = treeNodeStack.peek();
        //如果其右子树也为空，或者右子树已经访问
        //则可以直接输出当前节点的值
        if (node.right == null || node.right == lastVisit) {
            System.out.print(node.val + " ");
            treeNodeStack.pop();
            lastVisit = node;
            node = null;
        } else {
            //否则，继续遍历右子树
            node = node.right;
        }
    }
}

后序遍历结果

递归后序遍历： 7 8 6 4 2 5 3 1
非递归后序遍历：7 8 6 4 2 5 3 1

完整算法、用例 by Golang

package main

import "fmt"

type Node struct {
    V int
    L *Node
    R *Node
}
//前序
func forwardLook(root *Node)  {
    if root == nil {
        return
    }
    //输出行的位置在最前面
    fmt.Printf("node %v ", root.V)
    forwardLook(root.L)
    forwardLook(root.R)
}
//var i int
func forwardLoop(root *Node) {
    //需要一个堆保存走过的路径
    nodes:=[]*Node{}
    for len(nodes) !=  || root != nil {
        //一直往左走
        for root != nil{
            nodes=append(nodes, root)
            fmt.Printf("node %v ",root.V)
            root = root.L
        }
        //说明左子结点为空，那么就看右结点
        if len(nodes) > {
            root=nodes[len(nodes)-]
            //用完最近一个结点后，删除它，删除后最后的结点一定是父结点
            nodes=nodes[:len(nodes)-]
            //左子结点遍历完了，所以这里只看当看结点的右子结点
            root=root.R
        }else{
            root = nil
        }
    }
}
//中序
func middleLook(root *Node)  {
    if root == nil {
        return
    }
    middleLook(root.L)
    //输出行的位置在中间
    fmt.Printf("node %v ", root.V)
    middleLook(root.R)
}
//后序
func backwardLook(root *Node)  {
    if root == nil {
        return
    }
    //输出行的位置在后面
    backwardLook(root.L)
    backwardLook(root.R)
    fmt.Printf("node %v ", root.V)
}

func main(){
    tree:=&Node{,
        &Node{,
            &Node{, nil, nil}, &Node{, nil, nil},
            },
        &Node{,
            &Node{, nil, nil}, &Node{, nil, nil},
            },
    }
    fmt.Println("\nforwardLook ")
    forwardLook(tree)
    fmt.Println("\nforwardLoop ")
    forwardLoop(tree)
    fmt.Println("\nmiddleLook ")
    middleLook(tree)
    fmt.Println("\nbackwardLook ")
    backwardLook(tree)

    tree=&Node{,
        &Node{,
            nil,
            &Node{,
                nil,
                &Node{,
                    &Node{, nil, nil},
                    &Node{, nil, nil},
                    },
                },
            },
        &Node{,
            nil, &Node{, nil, nil},
            },
    }
    fmt.Println("\nforwardLook ")
    forwardLook(tree)
    fmt.Println("\nforwardLoop ")
    forwardLoop(tree)
    fmt.Println("\nmiddleLook ")
    middleLook(tree)
    fmt.Println("\nbackwardLook ")
    backwardLook(tree)
}

总结