在 Visual Studio 中安装 FxCop 分析器

本文转自 微软官网 ： https://docs.microsoft.com/zh-cn/visualstudio/code-quality/install-fxcop-analyzers?view=vs-2019

Microsoft 创建了一组名为CodeAnalysis的分析器，其中包含来自旧分析的最重要的 "FxCop" 规则。这些分析器检查代码中的安全性、性能和设计问题，等等。

您可以将这些 FxCop 分析器作为 NuGet 包或 VSIX 扩展安装到 Visual Studio。 若要了解每个的优缺点，请参阅NuGet 包与 VSIX 扩展。

NuGet 程序包

在 Visual Studio 2019 版本16.3 及更高版本中，你可以直接从项目的代码分析属性页安装CodeAnalysis FxCopAnalyzers NuGet 包：

1. 右键单击 "解决方案资源管理器中的项目节点，选择"属性"，然后选择"代码分析"选项卡。

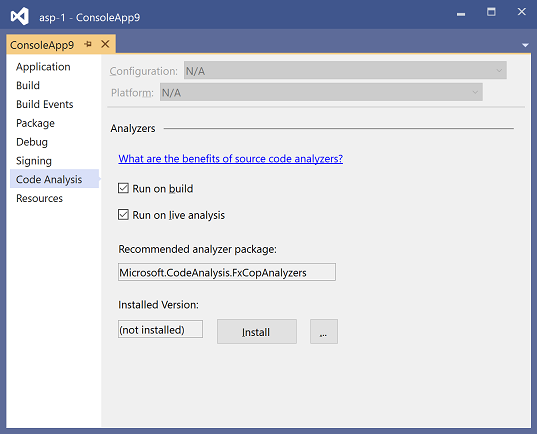
2. 选择“安装”。Visual Studio 将安装最新版本的 CodeAnalyzers。 FxCopAnalyzers 程序包。 程序集显示在 "引用 > 分析器" 下解决方案资源管理器中。

   如果使用的是较旧版本的 Visual Studio 2019，请使用程序包管理器控制台或包管理器 UI安装包。

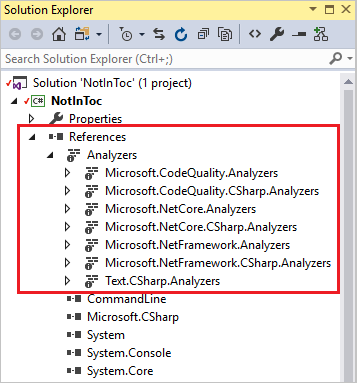
   自定义安装

   对于自定义安装，例如，若要指定不同版本的包，请在项目的 "代码分析" 属性页上选择省略号（"..."）按钮。 此按钮会将 "FxCopAnalyzers" 作为搜索字符串打开 NuGet 包管理器

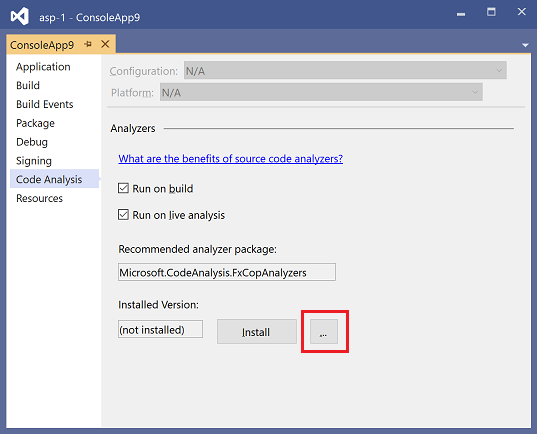
3. FxCopAnalyzers 包版本

   使用以下准则来确定要为你的 Visual Studio 版本安装的 FxCop 分析器包的版本：

   Visual Studio 版本	FxCop 分析器包版本
   Visual Studio 2019 （所有版本） Visual Studio 2017 版本15.8 及更高版本	最近
   Visual Studio 2017 版本15.5 到15。7	2.6.3
   Visual Studio 2017 版本15.3 到15。4	2.3.0-beta1
   Visual Studio 2017 版本15.0 到15。2	2.0.0-beta2
   Visual Studio 2015 update 2 和3	1.2.0-beta2
   Visual Studio 2015 Update 1	1.1.0
   Visual Studio 2015 RTW	1.0.1

   VSIX

   Microsoft 代码分析 2019扩展包含托管项目的所有 FxCop 分析器。 若要安装此扩展：

   1. 在 Visual Studio 中，选择 "扩展" > "管理扩展"。

      此时将打开 "管理扩展" 对话框。

      备注

      或者，直接从Visual Studio Marketplace下载扩展。

   2. 在左窗格中展开 "联机"，然后选择 " Visual Studio Marketplace"。

   3. 在搜索框中键入 "代码分析"，并查找Microsoft 代码分析 2019扩展。

      

   1. 选择 "下载"。

      此扩展已下载。

   2. 选择 "确定" 关闭对话框，然后关闭 Visual Studio 的所有实例以启动VSIX 安装程序。

      此时将打开 " VSIX 安装程序" 对话框。

   3. 选择 "修改" 以启动安装。

      一分钟或两分钟后，安装完成。

   4. 选择 "关闭"，然后重新打开 Visual Studio。

   如果要检查是否安装了扩展，请选择 "扩展" > "管理扩展"。 在 "管理扩展" 对话框中，选择左侧的 "已安装" 类别，然后按名称搜索扩展。