AngularJS2.0 quick start——其和typescript结合需要额外依赖

AngularJS2 发布于2016年9月份，它是基于ES6来开发的。

运行条件!

由于目前各种环境（浏览器或 Node）暂不支持ES6的代码，所以需要一些shim和polyfill（IE需要）让ES6写的代码能够转化为ES5形式并可以正常运行在浏览器中。

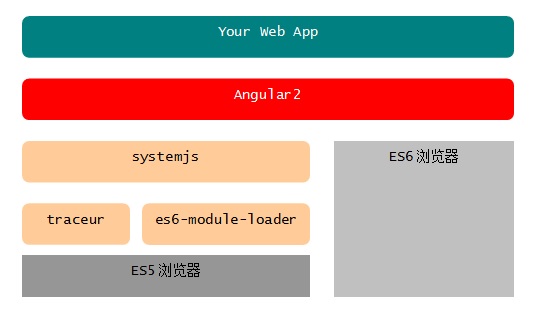
从上图可以看出在 Es5 浏览器下需要以下模块加载器：

• systemjs - 通用模块加载器，支持AMD、CommonJS、ES6等各种格式的JS模块加载。

• es6-module-loader - ES6模块加载器，systemjs会自动加载这个模块。

• traceur - ES6转码器，将ES6代码转换为当前浏览器支持的ES5代码，systemjs会自动加载 这个模块。

接下来

从零开始，通过TypeScript创建一个简单的应用程序。

可以看一下Angular2.0的官网给出的Demo https://angular.io

开发环境配置

我们需要一个应用程序项目文件夹，用来放一些库，一些TypeScript 的配置和所选的TypeScript-aware编辑器。

创建一个项目 angular2-quickstart

在磁盘下面创建一个目录：angular2-quickstart

在项目目录下面增加一个package.json的文件，文件内容如下：

{
  "name": "angular2-quickstart",
xxx，
  "dependencies": {
    "angular2": "2.0.0-beta.0",
    "systemjs": "0.19.6",
    "es6-promise": "^3.0.2",
    "es6-shim": "^0.33.3",
    "reflect-metadata": "0.1.2",
    "rxjs": "5.0.0-beta.0",
    "zone.js": "0.5.10"
  },
  "devDependencies": {
    "concurrently": "^1.0.0",
    "lite-server": "^1.3.1",
    "typescript": "^1.7.3"
  }
}

package.json文件编辑好之后 使用npm install安装。

配置 TypeScript

我们要引导TypeScript编译器非常详细的设置。

在项目根目录下面增加一个文件tsconfig.json，文件内容如下：xxx

到目前位置配置完成。

简单组件开发

在项目根目录下面建立一个app目录 ，便于存放源代码。 在app下面增加一个组件文件 app.component.ts文件内容如下：xxx

下面会告诉你如何调用上面的AppComponent组件。

在app目录下面增加一个boot.ts的文件，文件内容如下：

import {bootstrap}    from 'angular2/platform/browser'
import {AppComponent} from './app.component'

bootstrap(AppComponent);

boot.ts是用来运行这个组件的，需要两步来运行

1.导入 bootstrap 函数

2.导入我们刚才定义的AppComponent组件

调用 bootstrap 函数， 并传人主组件 AppComponent。

在项目根目录angular2-quickstart下面创建一个index.html文件。内容如下：xxx 见http://angularjs.cn/A2nG

运行Angular 2.0

然后在cmd下运行我们的app

npm start

运行出来竟然是

Loding.....

解决方法：在index.html中head里面其他script之前加入如下代码：

<script src="node_modules/es6-shim/es6-shim.js"></script>

参考：http://angularjs.cn/A2nG