UVa 806 四分树

题意：

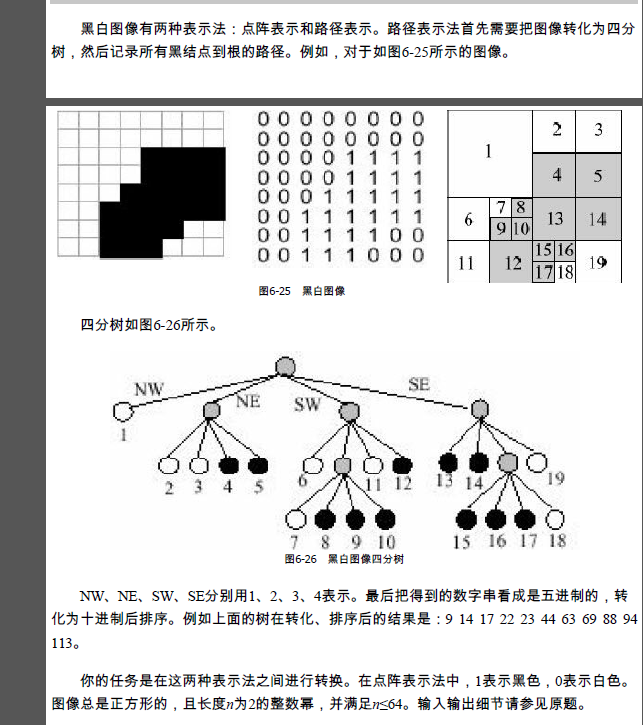
分析：

类似UVa 297， 模拟四分树四分的过程， 就是记录一个左上角， 记录宽度wideth， 然后每次w/2这样递归下去。 注意全黑是输出0， 不是输出1234。

 #include <bits/stdc++.h>
 using namespace std;
 // 1 2
 // 3 4
 const int base5[] = {,,,,,,,};
 int n;
 string G[];
 vector<int> code;
 int dfs(int r, int c, int w,int num,int dep){
     int lt[][] = {{},{r,c},{r,c+w/},{r+w/,c},{r+w/, c+w/}};

     for(int i = ; i <= ; i++){
         int all_black = , have_black = ;

         for(int j = lt[i][]; j < lt[i][] + w/; j++){
             for(int k = lt[i][]; k < lt[i][] + w/; k++){
                 if(G[j][k] == ''){
                     all_black = ;
                 }
                 else {
                     have_black = ;
                 }
             }
         }
         if(all_black == ){

             if(w == ){//宽度为2四分，只有一个格子， 只能为白
                 continue;
             }
             if(have_black)
                 dfs(lt[i][], lt[i][], w/, num + base5[dep]*i, dep +  );
         }
         else{
             code.push_back(num + base5[dep] * i);
         }
     }
 }
 void print(int r, int c, int w, int dep,int decode, int dec){
     int lt[][] = {{},{r,c},{r,c+w/},{r+w/,c},{r+w/, c+w/}};
     if(decode == ){
         for(int i = r; i < r + w; i++){
             for(int j = c; j < c + w; j++ ){
                 G[i][j] = '';
             }
         }
         return;
     }

     dec = decode % ;
     decode /= ;

     for(int i = ; i <= ; i++){
         if(dec == i){
             print(lt[i][], lt[i][], w/ , dep + ,decode, dec);
         }
         else continue;
     }
 }
 int main(){
     ios::sync_with_stdio(false);
     int kase = ;
     while(cin >> n && n){

         if(kase > ) cout <<'\n';
         cout << "Image "<<kase ++ << '\n';

         if(n > ){
             int flag = ;
             for(int i = ; i < n; i++){
                 cin >> G[i];
                 for(int j = ; j < G[i].size(); j++){
                     if(G[i][j] == '') flag = ;
                 }
             }
             if(!flag){//特判全黑
                 cout << "0\n";
                 cout << "Total number of black nodes = 1"<< "\n";
                 continue;

             }

             if(n == ){//特判n = 1 全白。
                 cout << "Total number of black nodes = 0" << "\n";
                 continue;
            }

             dfs(,,n,,);
             sort(code.begin(), code.end());
             for(int i = ; i < code.size(); i++){
                 cout << code[i];
                 if((i + ) %  ==  || i == code.size() - )
                     cout <<'\n';
                 else cout << ' ';
             }

             cout << "Total number of black nodes = "<< code.size() << '\n';
             code.clear();
         }

         else {
             n = -n;
             for(int i = ; i < n; i++){
                 G[i] = "";
                 G[i]. resize(n +);//string要更改size才能下标访问
             }
             int decode;
             while(cin >> decode && decode != -){
                 print(,,n,,decode, );
             }
             for(int i = ; i < n; i++){
                 for(int j = ; j < n; j++){
                     if(G[i][j] == ''){
                         cout << '*';
                     }
                     else cout << '.';
                 }
                 cout << '\n';
             }
         }
     }

     return ;
 }