KMP中next数组的理解与应用

理解

1、next数组一直往前走

next数组一直往前走，得到的所有前缀也是当前主串的后缀，当然了，也是当前主串的前缀。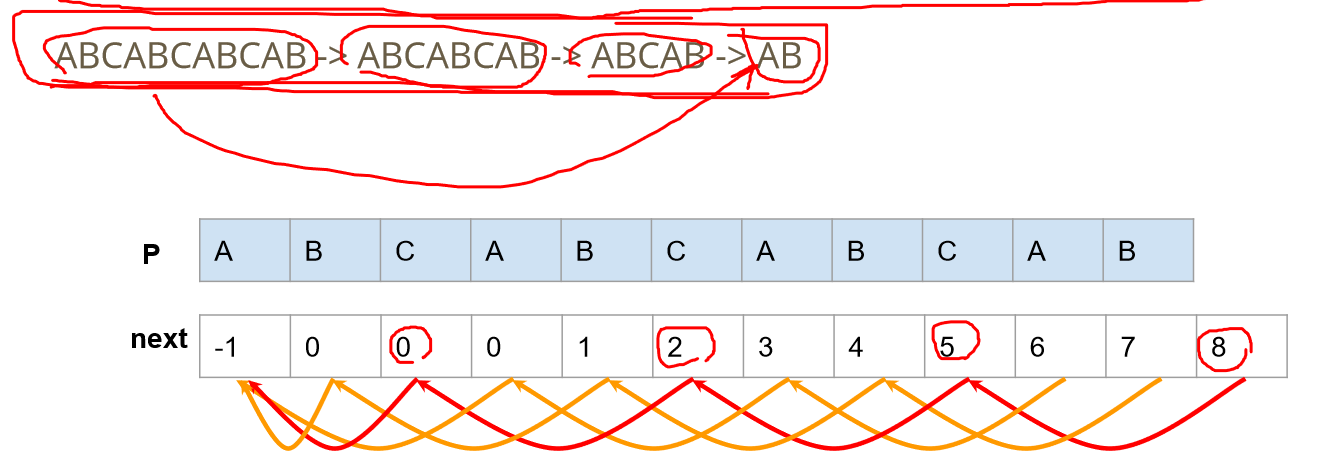

2、周期性字符串

1、周期性字符串$\Leftrightarrow n \,\% \, (n-next[n]) == 0 \ \&\& \ next[n] {\ } {\!}!{=} \  0 $，循环节长度是$n-next[n]$。

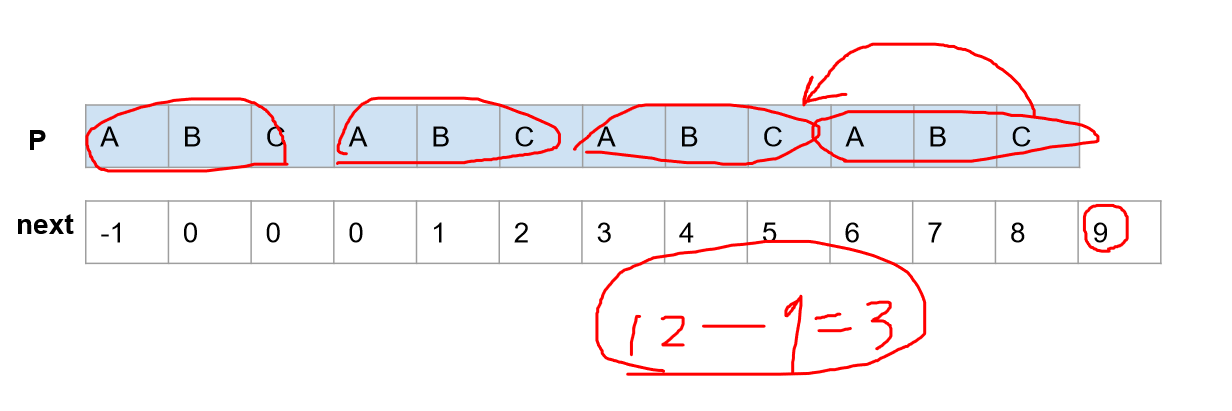
2、next数组往前跳的步长是一样的，除了最后一次。即$i-next[i]$保持恒定。

应用

• 题目一：Period

思路：先求出next数组，然后遍历一遍next数组得到所有字符结尾的字符串循环节的长度及个数

代码：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int maxn =  + ;
 int nexts[maxn],n;
 char s[maxn];

 void pre_kmp()
 {
     int i = , j = nexts[] = -;
     while (i < n)
     {
         while (j != - && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
     }
 }

 void slove()
 {
     pre_kmp();
     for(int i = ; i <= n; i++)
         if (i % (i - nexts[i]) ==  && nexts[i] != )  printf("%d %d\n", i, i / (i - nexts[i]));
 }

 int main()
 {
     int T = ;
     while (scanf("%d",&n) ==  && n)
     {
         scanf("%s", s);
         s[n] = '#';
         if (T)  printf("\n");
         printf("Test case #%d\n", ++T);
         slove();
     }
     return ;
 }

• 题目二：Power Strings

思路：先求next数组，再直接求循环节

代码：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int maxn =  + ;
 int nexts[maxn],n;
 char s[maxn];

 void pre_kmp()
 {
     int i = , j = nexts[] = -;
     //int n = strlen(s);
     while (i < n)
     {
         while (j != - && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
     }
 }

 void slove()
 {
     pre_kmp();
     if (n % (n - nexts[n]) != )  printf("1\n");
     else  printf("%d\n", n / (n - nexts[n]));
 }

 int main()
 {
     int T = ;
     while (scanf("%s", s) ==  && s[] != '.')
     {
         n = strlen(s);
         s[n] = '#';
         slove();
     }
     return ;
 }

• 题目三：Count The String

思路：求所有前缀出现的次数和，由于next数组回退得到的前缀也是主串的后缀，所以所有next回退的次数加上本身的一次取模就是答案。

代码：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int mod = ;
 const int maxn =  + ;
 int nexts[maxn], n;
 char s[maxn];

 void pre_kmp()
 {
     int i = , j = nexts[] = -;
     //int n = strlen(s);
     while (i < n)
     {
         while (j != - && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
     }
 }

 void slove()
 {
     int ans = n;
     pre_kmp();
     for (int i = n; i > ; i--)
     {
         int k = nexts[i];
         while (k > )
         {
             ans = (ans + ) % mod;
             k = nexts[k];
         }
     }
     printf("%d\n", ans);
 }

 int main()
 {
     int T;
     scanf("%d", &T);
     while (T--)
     {
         scanf("%d", &n);
         scanf("%s", s);
         slove();
     }
     return ;
 }

• 题目四：Cyclic Nacklace

思路：题目大意：问至少添加多少个字符，使得这个字符串有至少两个循环节。若本身有两个循环节返回0，否则补充至两个循环节。

代码：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int mod = ;
 const int maxn =  + ;
 int nexts[maxn], n;
 char s[maxn];

 void pre_kmp()
 {
     int i = , j = nexts[] = -;
     n = strlen(s);
     while (i < n)
     {
         while (j != - && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
     }
 }

 void slove()
 {
     pre_kmp();
     int len = n - nexts[n];
     if (n % len  ==  && nexts[n] != )  printf("0\n");
     else  printf("%d\n", len - nexts[n] % len);
 }

 int main()
 {
     int T;
     scanf("%d", &T);
     while (T--)
     {
         scanf("%s", s);
         slove();
     }
     return ;
 }

参考链接：

1、https://vjudge.net/contest/278481#overview

2、https://blog.csdn.net/hkh746392783/article/details/52015293