[POI2009]救火站Gas

Description

给你一棵树，现在要建立一些消防站，有以下要求: 1. 消防站要建立在节点上，每个节点可能建立不只一个消防站。 2. 每个节点应该被一个消防站管理，这个消防站不一定建立在该节点上。 3. 每个消防站可以管理至多s个节点。 4. 消防站只能管理距离（两点间最短路径的边数）不超过k的结点。请问至少要设立多少个消防站。

Input

第一行n,s,k。接下来n-1行每行xi,yi描述一条边连接xi与yi。 1<=n<=100000 1<=s<=n 1<=k<=20 1<=xi

Output

一个数，最少的消防站个数。

Sample Input

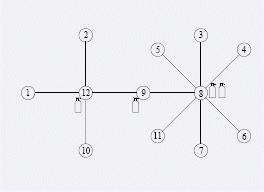
12 3 1

1 12

3 8

7 8

8 9

2 12

10 12

9 12

4 8

5 8

8 11

6 8

Sample Output

4

HINT

---

这题容易想到一个贪心策略，消防站必定先控制距离为k的点，然后距离递减，但是这个东西我们不好维护，所以我们就可以维护两个数组，用这两个数组来互相抵消维护。

转移的时候有一句话需要注意：

for (int i=k;i;i--)     more[x][i-1]+=more[son][i];

为什么是i来更新i-1，因为我控制的点有两个方向，一边向儿子，一边向父亲，向父亲方向的点显然要这么更新；由于儿子方向的点被两个数组互相抵消了两个距离的节点，所以这样更新是没有问题的

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int N=1e5,M=20;
int pre[(N<<1)+10],now[N+10],child[(N<<1)+10],tot;
ll more[N+10][M+10],need[N+10][M+10];
int n,m,k,Ans;
void join(int x,int y){pre[++tot]=now[x],now[x]=tot,child[tot]=y;}
void dfs(int x,int fa){
	need[x][0]=1;
	for (int p=now[x],son=child[p];p;p=pre[p],son=child[p]){
		if (son==fa)	continue;
		dfs(son,x);
		for (int i=0;i<k;i++)	need[x][i+1]+=need[son][i];
		for (int i=k;i;i--)		more[x][i-1]+=more[son][i];
	}
	int T=(need[x][k]+m-1)/m;
	Ans+=T;
	more[x][k]+=1ll*T*m;
	for (int i=0;i<=k;i++){
		if (more[x][i]){
			for (int j=i;~i&&(j>=i-1||x==1);j--){//抵消掉两个距离的节点
				if (more[x][i]<=need[x][j]){
					need[x][j]-=more[x][i];
					more[x][i]=0;
					break;
				}
				more[x][i]-=need[x][j];
				need[x][j]=0;
			}
		}
	}
}
int main(){
	n=read(),m=read(),k=read();
	for (int i=1;i<n;i++){
		int x=read(),y=read();
		join(x,y),join(y,x);
	}
	dfs(1,0);
	int tot=0;
	for (int i=0;i<=k;i++)	tot+=need[1][i];
	Ans+=(tot+m-1)/m;
	printf("%d\n",Ans);
	return 0;
}