bzoj1925 [Sdoi2010] 地精部落【DP】

传送门：http://www.lydsy.com/JudgeOnline/problem.php?id=1925

一个多月前“过”了这道题，还自欺欺人地认为懂了这道题，这直接导致了昨晚多校联测2的T3爆炸，现在想来简直是道水题，不过还是要有“懂得这题怎么做”的前提。。。地精部落这道题可以约化为另一个问题：对于n的排列，告诉你每个数相比于前一个数是大了、小了、还是都可以，求这样的排列的方案数。

先说这一题叭，看过很多其他人的题解，依然是云里雾里，因此我会写的详细一点。我的写法可能与其他人有些不同，但是本质是完全一样的。

首先令f(i, j)表示已经考虑完i的排列了，最后一个数是j，且它为山谷的方案数。这里特别注意！这个i的排列并不一定非要是闭区间[1, i]里的数！这种排列仅仅表示一个大小关系，一种相对的关系，有种离散化的感觉（也可以理解为考虑完i个数了，最后一个数是其中第j小的，且它为山谷的方案数）。这一点非常重要，一定要理解，如不理解可以先往下看，我后面会举个例子。类似地，令g(i, j)表示已经考虑完i的排列了，最后一个数是j，且它为山峰的方案数。那么状态转移方程就是：

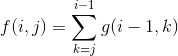    ①

为什么是这样呢？首先f数组的值一定是从g数组转移过来的，因为如果这个是山谷，那么上一个就是山峰。那么为什么等于后面那一串呢？考虑这个例子，7253，这是你填完最后一个数字3后的某个方案。很显然，这种方案应该属于状态f(4, 2)，因为已经考虑4个数了，3是其中第2小的。那么f(4, 2)这种状态可以从g(3, 2)与g(3, 3)转移过来，在7253这个例子中，f(4, 2)是从g(3, 2)转移过来的，因为在725中，5是第2小的。那么前i - 1个数中，最小能小到多少呢？（当然是考虑最小的，因为越大，就越可能转移到当前状态，所以最大能大到第i - 1小）答案是能小到j。因为前i个数中第j小的，必然比前i - 1个数中第j小的要小！可以通过刚刚7253这个例子来感受一下，3是前4个数中第2小的，5是前3个数中第2小的。

这个弄懂了之后，我们又可以发现一个很容易发现、非常显然的结论：把一个符合条件的n的排列，对于没一个数i，将其改为n + 1 - i，新的排列依然符合条件，并且原来的山峰变成山谷，山谷变成山峰，因此有：

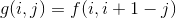   ②

联立①②，得

用一个辅助变量s，就可以O(1)转移了，最后ans = (f[n][1] + f[n][2] + ... + f[n][n]) * 2，因为f表示的是最后一个为山谷，根据那个显然的结论，可以得到等量的最后一个为山峰的方案数。在加一个滚动数组压缩空间就可以过了。

#include <cstdio>
#include <cstring>
 
const int maxn = 4205;
 
int n, p, f[2][maxn], s, ans;
 
int main(void) {
	scanf("%d%d", &n, &p);
	f[1][1] = 1;
	for (int i = 2; i <= n; ++i) {
		memset(f[i & 1], 0, sizeof f[0]);
		s = 0;
		for (int j = i - 1; j; --j) {
			s = (s + f[i & 1 ^ 1][i - j]) % p;
			f[i & 1][j] = s;
		}
	}
	for (int j = 1; j <= n; ++j) {
		ans = (ans + f[n & 1][j]) % p;
	}
	printf("%d\n", (ans << 1) % p);
	return 0;
}