bzoj1064【Noi2008】假面舞会

题意：http://www.lydsy.com/JudgeOnline/problem.php?id=1064

　　　给一个有向图染色，每个点的后继必须相同，问至少&至多有多少种染色方案

sol：  图由多个联通块组成，对于每个联通块，考虑以下3种情况：

　　　如果有环，分为3类讨论

　　　　　

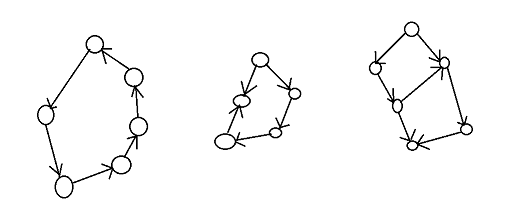
　　　　　对于第一种简单环，答案一定是环长的约数

　　　　　对于第二种有反向边的环，答案一定是两条链长差的约数

　　　　　　　trick：将有向边化为无向边，正向边权为1，反向为-1

　　　　　　　　　　这样1,2可以一起做

　　　　　对于第三种大环套小环，将小环缩点即可（gcd(a,b)=gcd(b,a-b)）

　　　　　所以答案最大为所有环长的gcd，最小为gcd的约数中>3的最小的一个

　　　如果是一个森林

　　　　　

　　　　　则答案最大值为深度之差的最大值，最小值为3

　　　若最大值<3则无解

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=;
const int M=;
int n,m,tot,maxn,minn,ansmin,ansmax;
int dis[N],head[N],vis[N],ver[M],nxt[M],edge[M];
void add(int u,int v,int d)
{
    tot++;
    nxt[tot]=head[u];
    ver[tot]=v;
    edge[tot]=d;
    head[u]=tot;
}
int gcd(int x,int y)
{
    if(!y) return x;
    return gcd(y,x%y);
}
void dfs1(int x,int fa)//找环
{
    vis[x]=;
    for(int i=head[x];i;i=nxt[i])
    {
        int v=ver[i];
        if(v!=fa)
        {
            if(!vis[v])vis[v]=,dis[v]=dis[x]+edge[i],dfs1(v,x);
            else ansmax=gcd(ansmax,abs(dis[x]-dis[v]+edge[i]));
        }
    }
}
void dfs2(int x,int fa)//处理森林
{
    vis[x]=;
    maxn=max(dis[x],maxn);
    minn=min(minn,dis[x]);
    for(int i=head[x];i;i=nxt[i])
    {
        int v=ver[i];
        if(v!=fa)
            if(!vis[v])
                vis[v]=,dis[v]=dis[x]+edge[i],dfs2(v,x);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    while(m--)
    {
        int a,b; scanf("%d%d",&a,&b);
        add(a,b,); add(b,a,-);
    }
    for(int i=;i<=n;i++) if(!vis[i]) dfs1(i,);
    if(ansmax) for(ansmin=;ansmin<=ansmax&&ansmax%ansmin;ansmin++);
    else
    {
        ansmin=;memset(vis,,sizeof(vis));
        for(int i=;i<=n;i++)
            if(!vis[i])
            {
                maxn=minn=,dis[i]=;
                dfs2(i,);ansmax+=maxn-minn+;
            }
    }
    if(ansmax<=) ansmax=ansmin=-;
    printf("%d %d\n",ansmax,ansmin);
    return ;
}