小匠第二周期打卡笔记-Task03

一、过拟合欠拟合及其解决方案

知识点记录

　　模型选择、过拟合和欠拟合：

　　　　训练误差和泛化误差：

　　　　　　训练误差 ：模型在训练数据集上表现出的误差，

　　　　　　泛化误差 ： 模型在任意一个测试数据样本上表现出的误差的期望，常常用测试数据集上的误差来近似。

　　　　　　二者的计算都可使用损失函数（平方损失、交叉熵）

　　　　　　机器学习模型应关注降低泛化误差

　　　　模型选择：

　　　　　　验证数据集：

　　　　　　　　训练数据集、测试数据集以外的一部分数据。简称验证集。

　　　　　　　　因不可从训练误差估计泛化误差，无法依赖训练数据调参（选择模型）。

　　　　　　　　测试数据集不可以用来调整模型参数，如果使用测试数据集调整模型参数，可能在测试数据集上发生一定程度的过拟合，此时将不能用测试误差来近似泛化误差。

　　　　　　K折交叉验证：

　　　　　　　　将原始训练数据集分割为K个不重合子数据集，之后做K次模型训练和验证。每次用一个子数据集验证模型，同时使用其他子数据集训练模型。最后将这K次训练误差以及验证误差各求平均数。

　　　　　　过拟合和欠拟合：

　　　　　　　　欠拟合：模型不能得到较低的训练误差。

　　　　　　　　过拟合：模型的训练误差<<其在测试数据集上的误差

　　　　　　　　发生欠拟合的时候在训练集上训练误差不能达到一个比较低的水平，所以过拟合和欠拟合不可能同时发生。

　　　　　　　　影响因素：

　　　　　　　　　　有多种因素，而且实践中要尽力同时掌控欠拟合和过拟合。这有两个重要因素：模型复杂度、训练数据集大小。

　　　　　　　　　　模型复杂度：在模型过于简单时，泛化误差和训练误差都很高——欠拟合。在模型过于复杂时，训练误差有了明显降低，但泛化误差会越来越高——过拟合。所以我们需要一个最佳值。如图像。

　　　　　　　　　　训练数据集大小：

　　　　　　　　　　　　训练数据集大小是影响着欠拟合和过拟合的一个重要因素。一般情况下，训练数据集中样本过少，会发生过拟合。但泛化误差不会随着训练数据集样本数的增加而增大。故在计算资源许可范围内，尽量将训练数据集调大一些。在模型复杂度较高（如：层数较多的深度学习模型）效果很好。

　　权重衰减：　　　

　　　　方法：正则化通过为模型的损失函数加入惩罚项，从而令得出的模型参数值较小。

　　　　权重衰减等价于L2范数正则化，经常用于应对过拟合现象。

　　　　L2范数正则化：

　　　　　　在模型原损失函数基础上添加L2范数惩罚项，从而的发哦训练所需最小化的函数。

　　　　　　　　L2范数惩罚项：模型权重参数每个元素的平方和与一个正的常数的乘积。　

　　　　　　范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。

　　丢弃法：

　　　　方法：在隐藏层每个单元设置丢弃的概率，如：p。那么有 p 的单元的概率就会被清零，有1-p的概率的单元会被拉伸。

　　　　丢弃法不改变输入的期望值。

　　　　在测试模型时，为了拿到更加确定性的结果，一般不使用丢弃法。丢弃法通过随机丢弃层间元素，使模型不依赖于某一个元素来应对过拟合的。

　　　　　　　　　　

梯度消失、梯度爆炸

知识点笔记

　　梯度消失和梯度爆炸：

　　　　深度模型有关数值稳定性的典型问题是梯度消失和梯度爆炸。当神经网络的层数较多时，模型的数值稳定性更容易变差。

　　　　层数较多时，梯度的计算也容易出现消失或爆炸。

　　随机初始化模型参数：

　　　　在神经网络中，需要随机初始化参数。因为，神经网络模型在层之间各个单元具有对称性。否则会出错。

　　　　若将每个隐藏单元参数都初始化为相等的值，则在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播中，每个隐藏单元的参数梯度相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代亦是如此。 据此，无论隐藏单元有几个，隐藏层本质上只有一个隐藏单元在发挥作用。所以，通常将神经网络的模型参数，进行随机初始化以避免上述问题。

　　　　PyTorch的默认随机初始化：

　　　　　　PyTorch中，nn.Module的模块参数都采取了较合理的初始化策略，一般不用考虑。

　　　　Xavier随机初始化：

　　　　　　Xavier随机初始化将使用该全连接层中权重参数的每个元素都随机采样于均匀分布U。模型参数初始化后，每层输出的方差不受该层输入个数影响，且每层梯度方差也不受该层输出个数影响。

　　考虑环境因素：

　　　　协变量偏移：

　　　　　　设虽输入的分布可能随时间而变，但标记函数（条件分布P（y|x））不会改变。但在实践中容易忽视。例如用卡通图片作为训练集训练猫狗的识别分类。在一个看起来与测试集有着本质不同的数据集上进行训练，而不考虑如何适应新的情况，这很糟糕。这种协变量变化是因为问题的根源在于特征分布的变化（协变量的变化）。数学上可以说P（x)变了，但P（y|x) 保持不变。当认为x导致y时，协变量移位通常是正确假设。

　　　　标签偏移：

　　　　　　导致标签偏移是标签P（y) 上的边缘分布的变化，但类条件分布是不变的P（x|y）是，会出现相反问题。当我们认为y导致x时，标签偏移是一个合理的假设。 病因（要预测的诊断结果）导致 症状（观察到的结果）。

　　　　　　训练数据集，数据很少且只包含流感p（y）的样本。而测试数据集有流感p（y）和流感q（y），其中不变的时流感症状p（x|y）。这里就认为发生了标签的偏移。

　　　　　概念偏移：

　　　　　　　相同的概念由于地理位置不同，标签本身的定义发生变化的情况。如果我们要建立一个机器翻译系统，分布P（y∣x）可能因我们的位置而异。这个问题很难发现。另一个可取之处是P（y∣x）通常只是逐渐变化。

　　　　　　

循环网络进阶

知识点记录：

　　GRU：

　　　　门控循环神经网络：　　　　

　　　　　　在循环神经网络中的梯度计算方法中，当时间步数较大后者时间步数较小时，循环神经网络的梯度容易出现梯度衰减或者梯度爆炸。裁剪梯度能应对梯度爆炸但无法解决梯度衰减问题。

　　　　　　门控循环神经网络，通过可以学习的门来控制信息的流动，更好捕捉时间序列中时间步距离较大的依赖关系。GRU（门控循环单元）就是一种常用的门控循环神经网络。

　　　　门控循环单元（GRU）：

　　　　　　重置门、更新门：　

　　　　　　　　门控循环单元中的重置门和更新门的输入均为当前时间步输入均为当前时间步输入Xt与上一时间步隐藏状态Ht-1。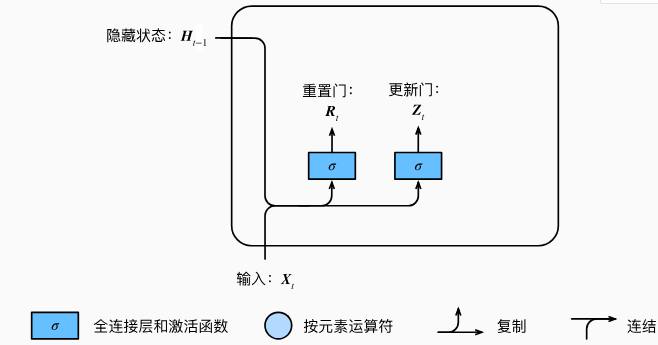

　　　　　　　　门控循环单元将计算候选隐藏状态来辅助稍后的隐藏状态计算。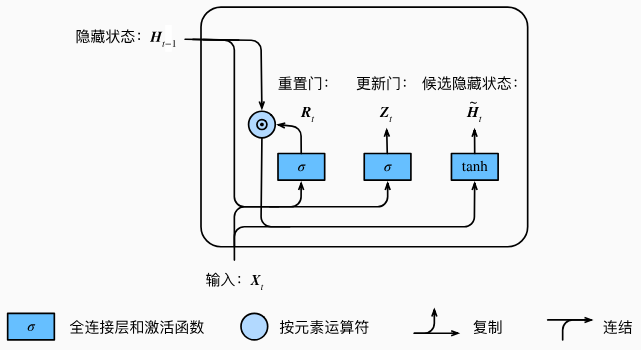　

　　　　　　　　更新门可以控制隐藏状态应该如何被包含当前时间步信息的候选隐藏状态所更新。这个设计可以应对循环神经网络中的梯度衰减问题，并更好地捕捉时间序列中时间步距离较大的依赖关系。

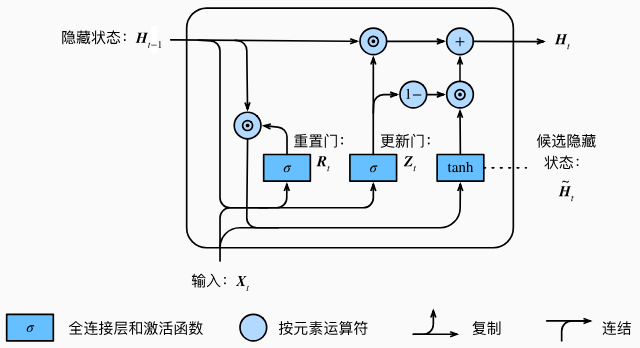
　　　　小结：

　　　　　　　　重置门有助于捕捉时间序列里短期的依赖关系；

　　　　　　　　更新门有助于捕捉时间序列里长期的依赖关系。

　　长短期记忆（LSTM）

　　　　引入三个门：输出门、遗忘门、输入门，以及与隐藏状态相同的记忆细胞，从而记录额外信息。

　　　　　　遗忘门:控制上一时间步的记忆细胞 输入门:控制当前时间步的输入
　　　　　　输出门:控制从记忆细胞到隐藏状态
　　　　　　记忆细胞：⼀种特殊的隐藏状态的信息的流动

　　　　　　长短期记忆的隐藏层输出包括隐藏状态和记忆细胞。只有隐藏状态会传递到输出层。

　　　　　　长短期记忆的输入门、遗忘门和输出门可以控制信息的流动。

　　　　　　长短期记忆可以应对循环神经网络中的梯度衰减问题，并更好地捕捉时间序列中时间步距离较大的依赖关系。

　　深度循环神经网络

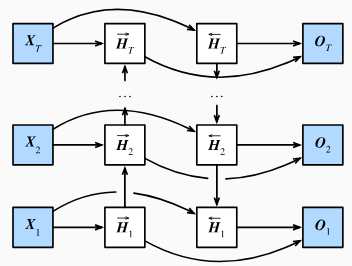
　　　　含有多个隐藏层的循环神经网络，也称作深度循环神经网络。有L个隐藏层的深度循环神经网络，每个隐藏状态不断传递至当前层的下一时间步和当前时间步的下一层。如下图：

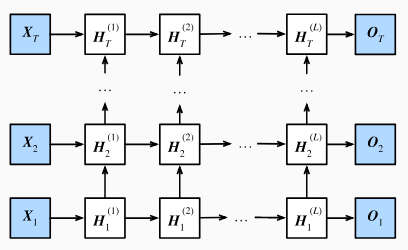
　　　　在深度循环神经网络中，隐藏状态的信息不断传递至当前层的下一时间步和当前时间步的下一层。

　　

　　　　双向循环神经网络

　　　　　　双向循环神经网络在每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列（包括当前时间步的输入）