PAT甲级——A1049 Counting Ones

The task is simple: given any positive integer N, you are supposed to count the total number of 1's in the decimal form of the integers from 1 to N. For example, given N being 12, there are five 1's in 1, 10, 11, and 12.

Input Specification:

Each input file contains one test case which gives the positive N (≤).

Output Specification:

For each test case, print the number of 1's in one line.

Sample Input:

12

Sample Output:

5

显然暴力枚举的方法是不可取的，我们需要寻找其中的规律，本题中可以分别计算出每一位的1出现的个数再进行加和。本博客中以数字N=345、N=305、N=315为例，寻找十位数字上是1的数字个数。将数字分成3部分：百位、十位、各位。
显然，从1~345这345个数中，百位数字可以出现0、1、2、3四种，每种百位数字都可以跟一个数字为1的十位，而每种十位数字可以跟0~9这十种数字，所以从1~345这345个数中，十位数字为1的数共有(3+1)×10=40 (3+1)×10=40(3+1)×10=40个，故十位上的1共出现40次。
当N=305时，百位数字依然可以出现0、1、2、3四种，但要注意，百位数字为3时，后面不能再跟数字为1的十位，因为这样的数字已经大于305了，所以从1~305这305个数中，十位数字为1的数共有3×10=30 3×10=303×10=30个，故十位上的1共出现30次。
当N=315时，百位数字依然可以出现0、1、2、3四种，此时要注意，百位数字为3时，后面可以再跟数字为1的十位，但这样的数字个位上只能出现0~5这6个数，即310、311、312、313、314、315，其他数字都会大于315，所以从1~315这315个数中，十位数字为1的数共有3×10+(5+1)=36 3×10+(5+1)=363×10+(5+1)=36个，故十位上的1共出现36次。

综上，对于任意一个数字N，当要判断从右向左数第i位上1出现的次数num时，可以将这个数字分成三部分，分别用left、current、right表示，即left=数字N在i位左侧的数字、current=数字N在第i位的数字、right=数字N在i位右侧的数字。例如数字N=123456，判断从右向左第2位也就是百位上，即数字4所在位置1出现的次数时，left=123、current=4、right=56。此时分三种情况进行计算：

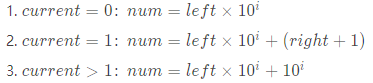
 #include <iostream>
 using namespace std;
 int main()
 {
     int n, ans = ;
     cin >> n;
     int left = n / , right = , cur = n % ;
     for (int i = ; right != n; i *= )
     {
         ans += left * i + (cur ==  ?  : cur ==  ? (right + ) : i);
         right += cur * i;
         cur = left % ;
         left /= ;
     }
     cout << ans << endl;
     return ;
 }