【BZOJ 2618】 2618: [Cqoi2006]凸多边形 （半平面交）

2618: [Cqoi2006]凸多边形

Description

逆时针给出n个凸多边形的顶点坐标，求它们交的面积。例如n=2时，两个凸多边形如下图：

则相交部分的面积为5.233。

Input

第一行有一个整数n，表示凸多边形的个数，以下依次描述各个多边形。第i个多边形的第一行包含一个整数m_i，表示多边形的边数，以下m_i行每行两个整数，逆时针给出各个顶点的坐标。

Output

输出文件仅包含一个实数，表示相交部分的面积，保留三位小数。

Sample Input

2
6
-2 0
-1 -2
1 -2
2 0
1 2
-1 2
4
0 -3
1 -1
2 2
-1 0

Sample Output

5.233

HINT

100%的数据满足：2<=n<=10，3<=m_i<=50，每维坐标为[-1000,1000]内的整数

半平面交模板：（终于缩到100行以内了。。。之前没删调试恶心的180+）

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 #define Maxn 1100

 struct P
 {
     double x,y;
     P() {x=y=;}
     P(double x,double y):x(x),y(y){}
     friend P operator - (P x,P y) {return P(x.x-y.x,x.y-y.y);}
     friend P operator + (P x,P y) {return P(x.x+y.x,x.y+y.y);}
     friend P operator * (P x,double y) {return P(x.x*y,x.y*y);}
     friend double operator * (P x,P y) {return x.x*y.y-x.y*y.x;}
     friend double operator / (P x,P y) {return x.x*y.x+x.y*y.y;}
 }a[Maxn];
 struct L
 {
     P a,b,v;double slop;
     friend bool operator < (L a,L b) {return (a.slop!=b.slop)?(a.slop<b.slop):a.v*(b.b-a.a)>;}
     friend P inter(L a,L b)
     {
         P nw=b.a-a.a;
         double tt=(nw*a.v)/(a.v*b.v);
         return b.a+b.v*tt;
     }
     friend bool jud(P x,L c) {return c.v*(x-c.a)<;}
 }l[Maxn],q[Maxn];int cnt,tot;

 void ffind()
 {
     for(int i=;i<=cnt;i++) l[i].v=l[i].b-l[i].a,l[i].slop=atan2(l[i].v.y,l[i].v.x);
     sort(l+,l++cnt);
     int L=,R=;
     tot=;
     for(int i=;i<=cnt;i++)
     {
         if(l[i].slop!=l[i-].slop) tot++;
         l[tot]=l[i];
     }
     cnt=tot;tot=;
     q[++R]=l[];q[++R]=l[];
     for(int i=;i<=cnt;i++)
     {
         while(L<R&&jud(inter(q[R-],q[R]),l[i])) R--;
         while(L<R&&jud(inter(q[L+],q[L]),l[i])) L++;
         q[++R]=l[i];
     }
     while(L<R&&jud(inter(q[R-],q[R]),q[L])) R--;
     while(L<R&&jud(inter(q[L+],q[L]),q[R])) L++;
     q[R+]=q[L];
     for(int i=L;i<=R;i++) a[++tot]=inter(q[i],q[i+]);
 }

 void init()
 {
     int n;
     scanf("%d",&n);
     cnt=;
     for(int i=;i<=n;i++)
     {
         int m;
         scanf("%d",&m);
         P ft,now,nw;
         scanf("%lf%lf",&ft.x,&ft.y);
         now=ft;
         for(int j=;j<=m;j++)
         {
             scanf("%lf%lf",&nw.x,&nw.y);
             l[++cnt].b=nw,l[cnt].a=now;
             now=nw;
         }
         l[++cnt].a=now;l[cnt].b=ft;
     }
 }

 void get_area()
 {
     double ans=;
     for(int i=;i<tot;i++) ans+=a[i]*a[i+];
     ans+=a[tot]*a[];
     if(tot<) ans=;
     printf("%.3lf\n",ans/);
 }

 int main()
 {
     init();
     ffind();
     get_area();
     return ;
 }

【分析】

　　然而只是想做一道半平面交的模版题，就从星期二打到了现在。。。【下午还要考试呢真是无爱。。

　　这题是求凸包的交，我们可以把每一条线段转化半平面，求半平面交。

　　对于半平面交，最朴素的想法应该是两两线段求交点，然后判断是否在每一个平面内，然后求凸包吧（感觉奇慢无比啊）

　　而事实上，如果有n的半平面的话，半平面交的答案那个凸包不会超过n条边，因为每个半平面最多只贡献一条边，说明我们事实上做了很多很多无用功。

　　根据凸包的思想，我们觉得半平面交也是有单调性的。

　　那个nlogn的算法可以看zzy的论文《半平面交的新算法及其实用价值》。

　　半平面共用向量表示，向量的左边为有效半平面。

　　定义半平面的极角为表示半平面的向量的极角。

　　根据半平面的极角进行排序，若两个半平面极角相同，明显只需要保存最靠左的半平面，根据这个去重。

　　然后这样做：

　　

　　

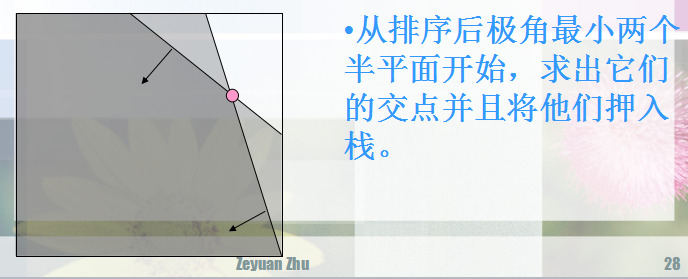
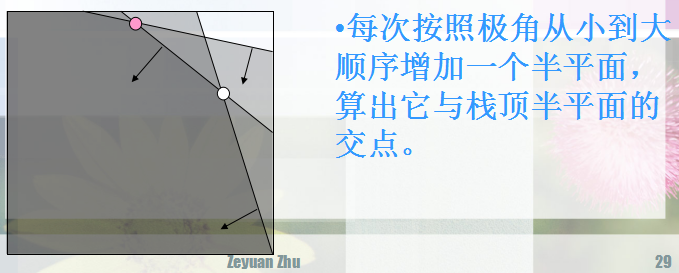
　　跟单调队列差不多，两边判断，删减。

　　

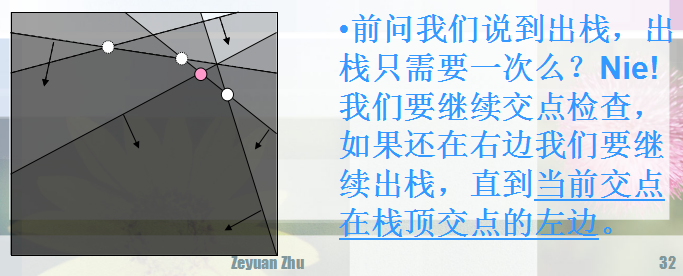
　　注意最后还要判断一下，去尾。像这样：

　　

　　

　　

　　

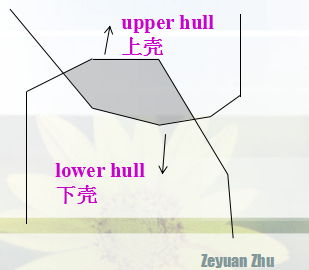
　　这题就是这样了。

放代码（调试很多，不删了）

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 #define Maxn 1100

 struct P {double x,y;};
 struct L {P a,b;double slop;}l[Maxn];
 //半平面只方向向量a->b的左部分
 //slop 极角
 int cnt;

 P operator - (P x,P y)
 {
     P tt;
     tt.x=x.x-y.x;
     tt.y=x.y-y.y;
     return tt;
 }

 P operator + (P x,P y)
 {
     P tt;
     tt.x=x.x+y.x;
     tt.y=x.y+y.y;
     return tt;
 }

 double Dot(P x,P y) {return x.x*y.x+x.y*y.y;}
 double Cross(P x,P y) {return x.x*y.y-x.y*y.x;}
 // bool operator < (L x,L y) {return x.slop<y.slop;}

 bool operator < (L a,L b)
 {
     if(a.slop!=b.slop)return a.slop<b.slop;
     return Cross(a.b-a.a,b.b-a.a)>;
 }

 P operator * (P X,double y)
 {
     P tt;
     tt.x=X.x*y;
     tt.y=X.y*y;
     return tt;
 }

 P a[Maxn];
 L q[Maxn];
 int tot;

 P inter(L a,L b)
 {
     P X=a.a-a.b,Y=b.a-b.b,nw;
     double tt;
     nw=b.a-a.a;
     tt=Cross(nw,X)/Cross(X,Y);
     P ans=b.a+Y*tt;
     return ans;
 }

 bool jud(L a,L b,L c)
 {
     P p=inter(a,b);
     return Cross(c.b-c.a,p-c.a)<;
 }

 void opp()
 {
     for(int i=;i<=cnt;i++)
     {
         printf("%.2lf %.2lf %.2lf %.2lf = %.2lf \n",l[i].a.x,l[i].a.y,l[i].b.x,l[i].b.y,l[i].slop);
     }
     printf("\n");
 }

 void output()
 {
     for(int i=;i<=tot;i++) printf("%2lf %.2lf\n",a[i].x,a[i].y);
     printf("\n");
 }

 void op(int L,int R)
 {
     for(int i=L;i<=R;i++)
         printf("%lf %lf %lf %lf\n",l[i].a.x,l[i].a.y,l[i].b.x,l[i].b.y);
     printf("\n");
 }

 void ffind()
 {
     for(int i=;i<=cnt;i++)
       l[i].slop=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x);
     sort(l+,l++cnt);

     // opp();

     int L=,R=;
     //去重？
     tot=;
     for(int i=;i<=cnt;i++)
     {
         if(l[i].slop!=l[i-].slop) tot++;
         l[tot]=l[i];
     }
     cnt=tot;tot=;
     // opp();
     q[++R]=l[];q[++R]=l[];
     for(int i=;i<=cnt;i++)
     {
         while(L<R&&jud(q[R-],q[R],l[i])) R--;
         while(L<R&&jud(q[L+],q[L],l[i])) L++;
         q[++R]=l[i];
         // op(L,R);
     }
     while(L<R&&jud(q[R-],q[R],q[L])) R--;
     while(L<R&&jud(q[L+],q[L],q[R])) L++;
     q[R+]=q[L];
     for(int i=L;i<=R;i++)
       a[++tot]=inter(q[i],q[i+]);
   // output();

   // output();
 }

 void init()
 {
     int n;
     /*scanf("%d",&n);
     for(int i=1;i<=n;i++)
     {
         scanf("%lf%lf%lf%lf\n",&l[i].a.x,&l[i].a.y,&l[i].b.x,&l[i].b.y);
     }
     cnt=n;*/
     scanf("%d",&n);
     cnt=;
     for(int i=;i<=n;i++)
     {
         int m;
         scanf("%d",&m);
         P ft,now;
         scanf("%lf%lf",&ft.x,&ft.y);
         now=ft;
         for(int j=;j<=m;j++)
         {
             P nw;
             scanf("%lf%lf",&nw.x,&nw.y);
             l[++cnt].b=nw;
             l[cnt].a=now;
             now=nw;
         }
         l[++cnt].a=now;l[cnt].b=ft;
     // opp();
     }

     for(int i=;i<=cnt;i++)
       l[i].slop=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x);
     // opp();

 }

 void get_area()
 {
     double ans=;
     for(int i=;i<tot;i++)
     {
         ans+=Cross(a[i],a[i+]);
     }
     ans+=Cross(a[tot],a[]);
     if(tot<) ans=;
     printf("%.3lf\n",ans/);
 }

 int main()
 {
     init();
     ffind();
     // output();
     get_area();
     return ;
 }

---

用向量法求两直线的交点：

本质就是用面积比表示线段比。

P inter(L a,L b)
{
	P X=a.a-a.b,Y=b.a-b.b,nw;
	double tt;
	nw=b.a-a.a;
	tt=Cross(nw,X)/Cross(X,Y);
	P ans=b.a+Y*tt;
	return ans;
}

半平面交核心过程：

q[++R]=l[1];q[++R]=l[2];
for(int i=3;i<=cnt;i++)
{
	while(L<R&&jud(q[R-1],q[R],l[i])) R--;
	while(L<R&&jud(q[L+1],q[L],l[i])) L++;
	q[++R]=l[i];
}
if(L<R&&jud(q[R-1],q[R],q[L])) R--;

　

代码的具体实现其实没有分上壳和下壳，是一起做的，每次保存有用的半平面，最后相邻的求交点形成凸包。

最后也不用处理上面去尾的情况了，但是注意加一句if，判断最后加的那个半平面是有效的。

：if(L<R&&jud(q[R-1],q[R],q[L])) R--;

【倒是对几何画板越来越熟练了，捂脸= =

2016-12-24 09:48:20