【poj1177】 Picture

http://poj.org/problem?id=1177 (题目链接)

题意

　　求矩形周长并。

Solution

　　转自：http://www.cnblogs.com/Booble/archive/2010/10/10/1847163.html

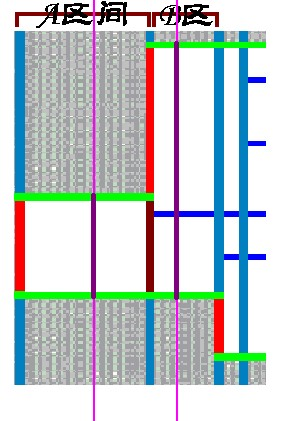
　　先看图：

　　

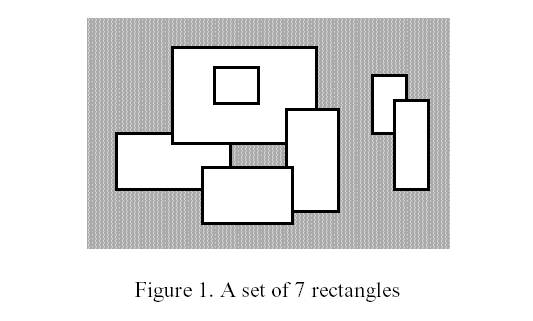
　　为了解决这个问题 我们先把一坨一坨的矩形 进行矩形切割：

　　

　　

　　

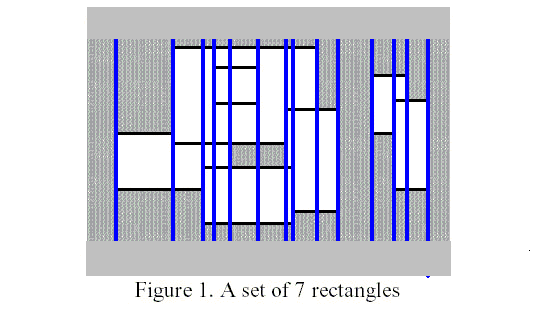
　　我们考虑周长由哪些部分构成

　　其中，红线是需要统计入周长的竖边，绿线是需要统计入周长的横边

　　我们称两条蓝线之间的部分为统计区间

　　我们需要依次统计从左到右的统计区间内的需要计数的矩形边，累加

　　形象地讲，就是用一根扫描线，从左到右依次扫描

　　具体实现就是依次遍历那些蓝线然后，累加每个区间的统计结果

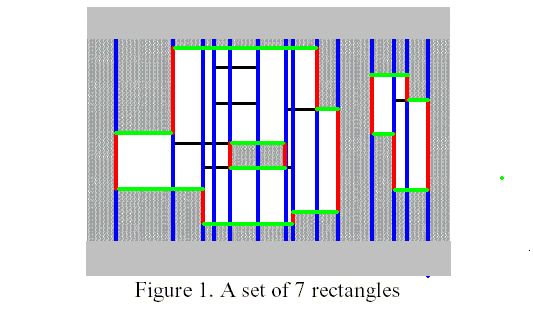
　　我们任取2个统计区间进行详细讨论，放大前2个统计区间部分

　　

　　考虑为什么同样是矩形边，红边需要统计而棕色的边不需要统计

　　我们发现深红色的边包含在第一个矩形内部，也就是夹在第一个矩形两条红边之间

　　继续分析，我们可以知道，横边也是这样

　　深蓝色边加在统计区间内的两条绿色边之间，属于矩形内部，不需要统计

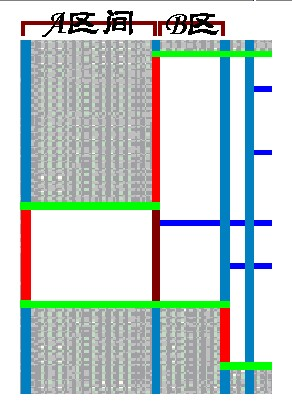
　　那么，如何判定是否是红边或绿边呢？

　　我们在扫描线上投下当前经过扫描线矩形的投影

　　

　　红边必然造成投影的变化，绿边必然在投影上线段的端点处

　　没有造成投影变化的竖边，肯定在投影内部，也就是在还未扫描完的矩形内部

　　

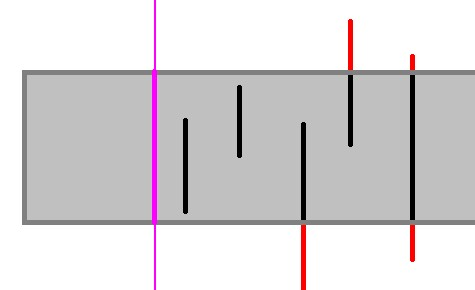
　　 不在投影线段段端点处的横边 也会夹在在投影线段端点处的两个矩形边内

　　

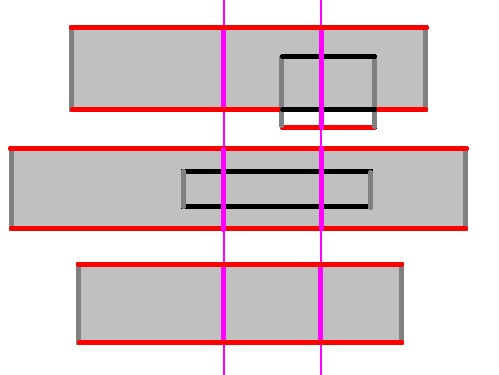
　　于是，我们将绿边的长度=统计区间宽*投影连续段数*2

　　再与红边的长度=与上一个区间投影的差求和，即得到当前区间的统计值，再累加即可

　　考虑怎么统计答案，我们采用线段树：

　　先将一个矩形一分为二，分别记录下左竖边，右竖边，差分。将竖边按照左端点排序，扫描线从左到右扫描，依次将竖边所在的区间加入线段树，统计答案。

　　用线段树记录下扫描线上的投影的情况

　　当扫描线碰到举行左边的时候就插入这个线段，碰到矩形右边就删除这个线段（差分）

　　我们还要重新规划在线段树上的域：覆盖次数cov[]，连续段数num[]，长度len[](即被覆盖的总长度)

　　这几个域需要我们实时维护，更需增加维护的域ls[]，rs[]表示左右端点是否被覆盖

　　于是问题至此就差不多解决了，注意我们线段树上记录的是区间而不是端点，这样更方便我们统计答案。

细节

　　左右下标。

代码

// poj1177
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define inf 2147483640
#define Pi acos(-1.0)
#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;

const int maxn=20010;
struct tree {int l,r,len,ls,rs,num,cov;}tr[maxn<<2];
struct data {int x,l,r,val;}a[maxn];
int n;

void build(int k,int s,int t) {
    tr[k].l=s;tr[k].r=t;
    if (s==t) return;
    int mid=(s+t)>>1;
    build(k<<1,s,mid);
    build(k<<1|1,mid+1,t);
}
void merge(int k) {
    int l=tr[k].l,r=tr[k].r;
    if (tr[k].cov) {
        tr[k].ls=tr[k].rs=1;
        tr[k].num=2;
        tr[k].len=r-l+1;
    }
    else if (l==r) tr[k].ls=tr[k].rs=tr[k].len=tr[k].num=0;
    else {
        tr[k].num=tr[k<<1].num+tr[k<<1|1].num;
        tr[k].len=tr[k<<1].len+tr[k<<1|1].len;
        tr[k].ls=tr[k<<1].ls;tr[k].rs=tr[k<<1|1].rs;
        if (tr[k<<1].rs && tr[k<<1|1].ls) tr[k].num-=2;
    }
}
void update(int k,int s,int t,int val) {
    int l=tr[k].l,r=tr[k].r,mid=(l+r)>>1;
    if (s<=l && t>=r) {tr[k].cov+=val;merge(k);return;}
    if (s<=mid) update(k<<1,s,t,val);
    if (t>mid) update(k<<1|1,s,t,val);
    merge(k);
}
bool cmpx(data a,data b) {
    return a.x<b.x;
}
int main() {
    scanf("%d",&n);
    int m=0,l=inf,r=-inf;
    for (int x1,x2,y1,y2,i=1;i<=n;i++) {
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        l=min(l,y1);r=max(r,y2);
        a[++m]=(data){x1,y1,y2,1};a[++m]=(data){x2,y1,y2,-1};
    }
    n=m;
    build(1,l,r-1);
    sort(a+1,a+1+n,cmpx);
    int ans=0;
    for (int i=1;i<=n;i++) {
        int tmp=tr[1].len;
        if (i!=1) ans+=tr[1].num*(a[i].x-a[i-1].x);
        update(1,a[i].l,a[i].r-1,a[i].val);
        ans+=abs(tr[1].len-tmp);
    }
    printf("%d",ans);
    return 0;
}