[CTSC2018]暴力写挂——边分树合并

[CTSC2018]暴力写挂

题面不错

给定两棵树，两点“距离”定义为：二者深度相加，减去两棵树上的LCA的深度（深度指到根节点的距离）

求最大的距离。

解决多棵树的问题就是降维了。

经典的做法是边分树合并。

边分树结构类似0/1 trie

就是把边分树对于每个点拆开路径

合并两棵边分树同时可以得到两个边分树之间点对的路径的信息

感觉有点类似线段树合并。

根据“猫树”思想，两点间的路径一定经过边分树上LCA的那条边。（u，v不相等）

我们考虑在这个LCA处统计贡献

具体地，先对1树进行边分治

每个点初始的边分树是一条链，考虑对每个点构造出这个边分树。

开始只有根。

其实就是记录分治时候是在那个位置。

定义连接分治重心root深度较小的连通块为右部点，另一个为左部点

保存每个点作为左部点还是右部点

在每个之前最后一个加入位置lasi 下面加入左儿子或者右儿子。

在lasi位置保留这个信息vl，vr。初始是-inf

表示子树里所有的真实点在边分治这一层的左部、右部最大值。

左部点贡献权值：dis[x]

右部点贡献：dis[x]-dis[lca]

因为lca一定在右部点。

在第二棵树上枚举LCA z ，子树边分树合并上来（就类似树上的线段树合并）

合并时候max(vl(x)+vr(y)-dis'[z],vr(x)+vl(y)-dis'[z])更新答案。

然后vl(x)=max(vl(x),vl(y)) vr同理。按位取max

（注意没有pushup，因为这里是分治结构）

可以发现，任意点对(u,v)，一定在第二棵树上的LCA位置被考虑到，边分树合并时候，会在边分树LCA处尝试做出贡献。

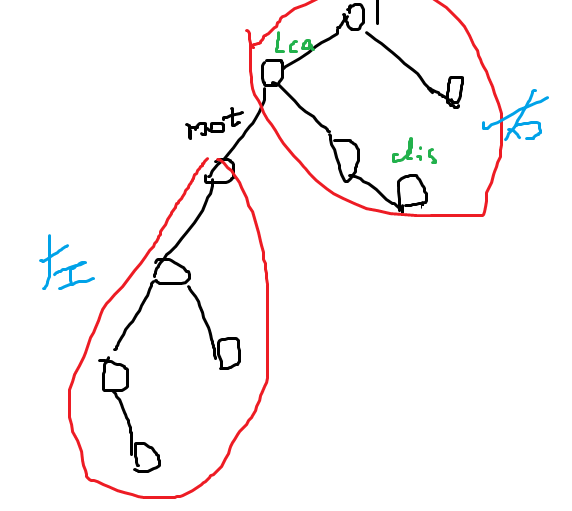
大概初始的分治树：

代码：

注意：

1.边分树2*N个点，边数4*N，

边分治的vis数组开4*N。

2.处理u,v重合情况。

// luogu-judger-enable-o2
// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}

namespace Miracle{
const int N=+;
const ll inf=1e18;
int n;

struct tr{
    int ls,rs;
    ll vl,vr;
    tr(){
        ls=;rs=;vl=vr=-inf;
    }
}t[N*];
ll ans;
int tot;
int rt[N];
ll nd;//now dis of lca'(u,v)
int merge(int x,int y){
    // cout<<" merge "<<x<<" "<<y<<endl;
    if(!x||!y) return x+y;
    ans=max(ans,max(t[x].vl+t[y].vr,t[x].vr+t[y].vl)-nd);
    t[x].ls=merge(t[x].ls,t[y].ls);
    t[x].rs=merge(t[x].rs,t[y].rs);
    t[x].vl=max(t[x].vl,t[y].vl);
    t[x].vr=max(t[x].vr,t[y].vr);
    return x;
}

namespace tr1{
vector<int>to[N],val[N];
ll dis[*N];
struct node{
    int nxt,to;
    int val;
}e[*N];
int hd[*N],cnt=;
void add(int x,int y,int z){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
    e[cnt].val=z;
}
int cur;
int d[*N];
void rebuild(int x,int fa){
    int las=x;
    for(reg i=;i<(int)to[x].size();++i){
        int y=to[x][i];
        if(y==fa) continue;
        ++cur;
        add(las,cur,);
        add(cur,las,);
        add(cur,y,val[x][i]);
        add(y,cur,val[x][i]);
        las=cur;
        rebuild(y,x);
    }
}
void dfs(int x,int fa){
    // cout<<" dfs tr1 "<<x<<" "<<fa<<endl;
    d[x]=d[fa]+;
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dis[y]=dis[x]+e[i].val;
        dfs(y,x);
    }
}
int nowsz;
int vis[*N];
int las[*N];
int root,sz[*N];
int mi;
void fin(int x,int fa){
    sz[x]=;
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(vis[i]||y==fa) continue;
        fin(y,x);
        if(mi>max(sz[y],nowsz-sz[y])){
            mi=max(sz[y],nowsz-sz[y]);
            root=i;
        }
        sz[x]+=sz[y];
    }
}
void dfs2(int x,int fa,int id,int typ){//min d's id//typ==0 : le ; typ==1 ri
    sz[x]=;
    if(d[id]>d[x]) id=x;
    if(x<=n){
        if(typ==){
            ++tot;
            t[las[x]].ls=tot;
            t[las[x]].vl=dis[x];
            las[x]=tot;
        }else{
            ++tot;
            t[las[x]].rs=tot;
            t[las[x]].vr=dis[x]-dis[id];
            las[x]=tot;
        }
    }

    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(vis[i]||y==fa) continue;
        dfs2(y,x,id,typ);
        sz[x]+=sz[y];
    }
}
void divi(int x){
    if(nowsz==) return;
    root=;
    mi=0x3f3f3f3f;
    fin(x,);
    // cout<<" root "<<root<<" x "<<x<<endl;
    int le=e[root].to,ri=e[root^].to;
    if(d[le]<d[ri]) swap(le,ri);
    // cout<<" le "<<le<<" ri "<<ri<<endl;

    vis[root]=vis[root^]=;
    dfs2(le,,,);
    dfs2(ri,,,);
    nowsz=sz[le];
    divi(le);
    nowsz=sz[ri];
    divi(ri);
}
void che(int x){
    if(!x) return;
    cout<<" nowcur "<<x<<endl;
    cout<<" vl "<<t[x].vl<<" vr "<<t[x].vr<<" ls "<<t[x].ls<<" rs "<<t[x].rs<<endl;
    che(t[x].ls);che(t[x].rs);
}
void main(){
    int x,y,z;

    for(reg i=;i<n;++i){
        rd(x);rd(y);rd(z);
        to[x].push_back(y);val[x].push_back(z);
        to[y].push_back(x);val[y].push_back(z);
    }
    cur=n;
    rebuild(,);
    // cout<<" rb "<<endl;
    dfs(,);
    // prt(dis,1,cur);
    // prt(d,1,cur);
    // cout<<" dfs "<<endl;
    d[]=0x3f3f3f3f;

    nowsz=cur;
    for(reg i=;i<=n;++i){
        rt[i]=++tot;
        las[i]=tot;
    }
    divi();
    // che(3);
    // che(4);

    // cout<<" divi "<<endl;
}

}
namespace tr2{
ll dis[N];
struct node{
    int nxt,to;
    int val;
}e[*N];
int hd[N],cnt=;
void add(int x,int y,int z){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
    e[cnt].val=z;
}
void dfs(int x,int fa){
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dis[y]=dis[x]+e[i].val;
        dfs(y,x);
        nd=dis[x];
        // cout<<" xx "<<x<<" nd "<<nd<<endl;
        rt[x]=merge(rt[x],rt[y]);
    }
    ans=max(ans,tr1::dis[x]-dis[x]);
}
void main(){
    int x,y,z;
    for(reg i=;i<n;++i){
        rd(x);rd(y);rd(z);
        add(x,y,z);add(y,x,z);
    }
    ans=-inf;
    dfs(,);
}

}
int main(){
    rd(n);
    tr1::main();
    tr2::main();
    ot(ans);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2019/4/13 19:58:12
*/

合并时候，就是利用分治树的结构层层分离点对，在分治边的位置贡献。

进行降维。