[HNOI2012]与非

题目描述

NAND（与非）是一种二元逻辑运算，其运算结果为真当且仅当两个输入的布尔值不全为真。NAND运算的真值表如下（1表示真，0表示假）:

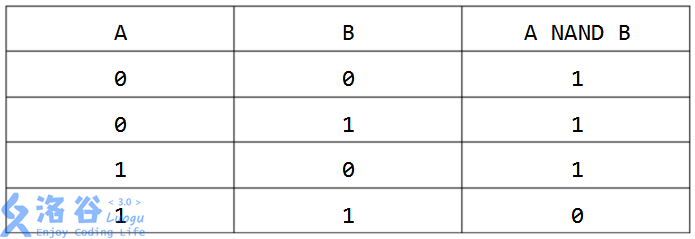
两个非负整数的NAND是指将它们表示成二进制数，再在对应的二进制位进行NAND运算。由于两个二进制数的长度可能不等，因此一般约定一个最高位K，使得两个数的二进制表示都不 超过K位，不足K位的在高位补零。给定N个非负整数A1,A2......AN和约定位数K，利用NAND运算与括号，每个数可以使用任意次，请你求出范围[L,R]内可以被计算出的数有多少个。

输入输出格式

输入格式：

输入文件第一行是用空格隔开的四个正整数N，K，L和R，接下来的一行是N个非负整数A1,A2......AN，其含义如上所述。 100%的数据满足K<=60且N<=1000,0<=Ai<=2^k-1,0<=L<=R<=10^18

输出格式：

仅包含一个整数，表示[L,R]内可以被计算出的数的个数

输入输出样例

输入样例#1： 复制

3  3 1 4
3  4 5

输出样例#1： 复制

4

说明

样例1中，(3 NAND 4) NADN (3 NAND 5) = 1，5 NAND 5 = 2，3和4直接可得。

可以表示出其他所有的位运算

$not\ A=A\ nand\ A$

$A\ and\ B=not\ (A\ nand\ B)$

$A\ or\ B=(not\ A)\ nand\ (not\ B)$

$A\ xor\ B=(A\ and\ not\ B)\ or\ (not\ A\ and\ B)$

所以相当于是这$n$ 个数之间可以做任何位运算。

如果这$n$ 个数中每个数的第$i$ 位和第$j$ 位都相同，那么这$n$ 个数无论怎么运算，最后得到的答案中第$i$ 位和第$j$ 位一定相同

然后就是数位dp

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef long long lol;
 lol tmp[],c[],cnt[],Q[][];
 lol a[],k,n,L,R;
 lol dfs(lol s,lol x,lol flag)
 {lol i,j;
   if (x<) return ;
   if (!flag)
   {
     memcpy(tmp,c,sizeof(c));
     lol tot=;
     for (i=x;i>=;i--)
       if (tmp[i]==-)
       {
         tot++;
         for (j=;j<=cnt[i];j++)
           {
             tmp[Q[i][j]]=;
           }
       }
     return 1ll<<tot;
   }
   lol ed=((s>>x)&);
   lol sum=;
   if (c[x]==-)
     {
       for (i=;i<=ed;i++)
         {
           for (j=;j<=cnt[x];j++)
             {
               c[Q[x][j]]=i;
             }
           sum+=dfs(s,x-,flag&(i==ed));
         }
       for (j=;j<=cnt[x];j++)
         {
       c[Q[x][j]]=-;
         }
       return sum;
     }
   else
     {
       if (flag&&c[x]&&ed==) return ;
       return dfs(s,x-,flag&(c[x]==ed));
     }
 }
 lol solve(lol s)
 {
   memset(c,-,sizeof(c));
   if (s<) return ;
   return dfs(s,k-,(s>>k)?:);
 }
 int main()
 {lol i,j,l,flag;
   cin>>n>>k>>L>>R;
   for (i=;i<=n;i++)
     scanf("%lld",&a[i]);
   for (i=k-;i>=;i--)
     {
       for (j=i-;j>=;j--)
         {
           flag=;
           for (l=;l<=n;l++)
             if (((a[l]>>i)&)^((a[l]>>j)&))
               {
             flag=;break;
               }
           if (flag==)
             Q[i][++cnt[i]]=j;
         }
       Q[i][]=i;
     }
   printf("%lld\n",solve(R)-solve(L-));
 }