汉诺塔I && II

汉诺塔I

题目链接：https://www.nowcoder.com/questionTerminal/7d6cab7d435048c4b05251bf44e9f185

题目大意：

　　略

分析：

　　利用汉诺塔与二进制的关系来做。

　　如何用二进制解汉诺塔：https://www.bilibili.com/video/av7398130/

代码如下：

 class Hanoi {
 public:
     // 计算x的二进制位数
     inline int getBits(int x) {
         int cnt = ;
         while(x >>= ) ++cnt;
         return cnt;
     } 
 
     vector<string> getSolution(int n) {
         vector< string > ans;
         string s[] = {"left", "mid", "right"};
         vector< int > arr;
         arr.resize(n, );
         // tot表示总移动次数
         int tot = ( << n) - ;
         int cnt = ;
         while(cnt++ < tot) {
             int lowbit = cnt & (-cnt);
             int bitlen = getBits(lowbit) - ;
             int b =  + (n - bitlen) % ;// 偏移，b = 1往右，b = 2往左
             ans.push_back("move from " + s[arr[bitlen]] + " to " + s[(arr[bitlen] + b) % ]);
             arr[bitlen] = (arr[bitlen] + b) % ;
         }
         return ans;
     }
 };

汉诺塔II

题目链接：https://www.nowcoder.com/questionTerminal/b2d552cd60b7415fad2612a32e799812?toCommentId=2927834

题目大意：

　　略

分析：

先给出4个盘子的表（三根柱子的序号分别为0， 1， 2）：

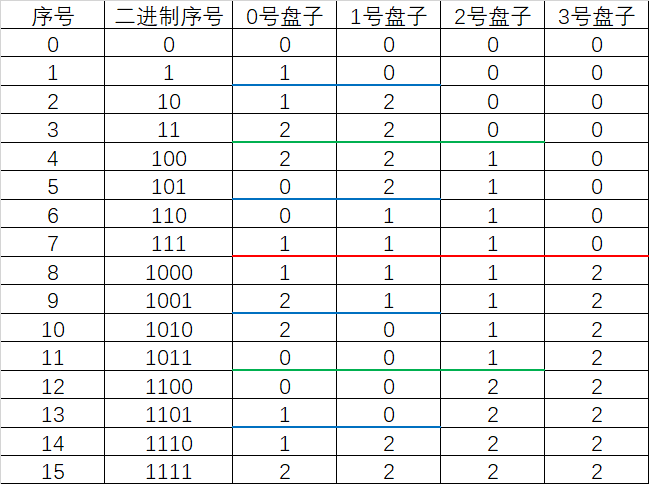
容易看出n个盘子需要移动2ⁿ次。

　　首先我们看红线分割的两块，令8~15行的0号，1号，2号盘子的位置加上2再模3，他们的数值刚好等于0~7行的0号，1号，2号盘子的位置。

　　再看绿线分割的0~7行，另4~7行的0号，1号盘子的位置加上1再模3，他们的数值刚好等于0~3行的0号，1号盘子的位置。

　　发现规律了没有？

　　比如有汉诺塔的位置序列[2, 1, 1, 2]，序列最后一个数为2，于是step([2, 1, 1, 2])就等于1000_B + step([(2 + 2) % 3, (1 + 2) % 3,  (1 + 2) % 3]) = 1000_B + step([1, 0, 0])，然后step([1, 0, 0])的最后一个数为0，于是step([1, 0, 0]) = step([1， 0])，直接往前进，并不需要上移，同理step([1， 0]) = step([1])， 对于step([1])，只有一个数字，直接取值，所以step([2, 1, 1, 2])最终等于1001_B。

　　再比如有汉诺塔的位置序列[2, 0, 1, 2]，序列最后一个数为2，于是step([2, 0, 1, 2])就等于1000_B + step([(2 + 2) % 3, (0 + 2) % 3,  (1 + 2) % 3]) = 1000_B + step([1, 2, 0])，然后step([1, 2, 0])的最后一个数为0，于是step([1, 2, 0]) = step([1, 2])，step([1, 2])的最后一个数字是2，于是step([1, 2]) = 10_B + step([(1 + 2) % 3]) = 10_B + step([0])， 对于step([0])，只有一个数字，直接取值，所以step([2, 1, 1, 2])最终等于1010_B。

　　简单来说，就是末尾数字为0，就不变；末尾数字不为0，就让前面的数字加上这个数字再模3，然后求子问题，同时要加上这一位的权值，比如它是第5个数字，就要加上10000_B；如果是第3个数字，就要加上100_B。

　　不要问我原理，我是结合二进制找规律找出来的。

代码如下：

 class Hanoi {
 public:
     int chkStep(vector<int> &arr, int n, int b = ) {
         if(n == ) return ;
         int tmp = (arr[n - ] + b - ) %  ;
         return ( << (n - )) * (tmp != ) + chkStep(arr, n - , b + tmp);
     }
 };