决策树-C4.5算法（三）

在上述两篇的文章中主要讲述了决策树的基础，但是在实际的应用中经常用到C4.5算法，C4.5算法是以ID3算法为基础，他在ID3算法上做了如下的改进：

　1) 用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足，公式为GainRatio(A)；

　　2) 在树构造过程中进行剪枝；

　　3) 能够完成对连续属性的离散化处理；

　　4) 能够对不完整数据进行处理。

　　C4.5算法与其它分类算法如统计方法、神经网络等比较起来有如下优点：产生的分类规则易于理解，准确率较高。其缺点是：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。

1.信息增益率

之所以是用信息增益率起原因是信息增益在选择属性时会偏向多属性这个缺点：

信息增益率定义如下：

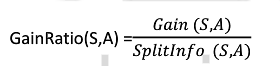
其中Grain(S,A) 与ID3的信息增益相同，而分裂信息SplitInfo（S,A）代表了按照属性A分裂样本集的广度与均匀性。

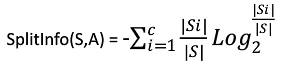
其中S1到Sc是C个不同值得属性A分割中S而形成的C个样本子集，如果按照属性A把S集（30个用列）分成10与20个用列集合，则SplitInfo（S,A）= -1/3*log（1/3）-2/3log(2/3)

2.以二值离散的方式处理连续型的数据

所谓二值离散：是指对连续属性进行排序，得到多个候选阈值，选取产生最大信息增益的阈值作为分裂阈值

3.C4.5采用的改进EBP剪枝算法

4.处理缺失值

在ID3算法中不能处理缺失值，而本算法可却可以，处理缺失值得方法如下：

以上是C4.5 算法的相对于ID3算法的改进。

其中在C4.5之后又发展了C5.0算法，引入了Boost框架。具体可以看相关的附件。

参考： http://blog.csdn.net/zhoubl668/article/details/40828573

来自为知笔记(Wiz)