Armijo-Goldstein准则与Wolfe-Powell准则

Armijo-Goldstein准则与Wolfe-Powell准则是不精确的一维搜索的两大准则。

之所以要遵循这些准则是为了能使算法收敛（求最优解）。即要使我们的不精确的一维搜索的步长满足一定的规则，使之后的求最优解的过程不至于因为步长过大或者过小而不收敛。

Armijo-Goldstein准则

Armijo-Goldstein准则的核心思想有两个：①目标函数值应该有足够的下降；②一维搜索的步长α不应该太小。

我们来看看Armijo-Goldstein准则的数学表达式：

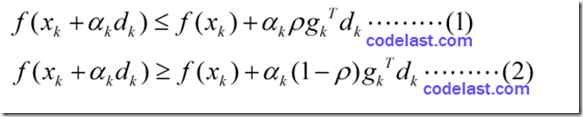
其中， 0<ρ<12

1)为什么要规定 ρ∈(0,0.5) 这个条件？其实可以证明：如果没有这个条件的话，将影响算法的超线性收敛性。具体的证明过程，大家可以参考袁亚湘写的《最优化理论与方法》一书，我没有仔细看，我觉得对初学者，不用去管它。
(2)第1个不等式的左边式子的泰勒展开式为：
f(x_k+α_kd_k)=f(x_k)+α_kg_k^Td_k+o(α_k)
去掉高阶无穷小，剩下的部分为： f(x_k)+α_kg_k^Td_k
而第一个不等式右边与之只差一个系数 ρ
我们已知了 g_k^Td_k<0 （这是 d_k 为下降方向的充要条件），并且 ρ∈(0,0.5) ，因此，1式右边仍然是一个比 f(x_k) 小的数，即：
f(x_k)+α_kρg_k^Td_k<f(x_k)
也就是说函数值是下降的（下降是最优化的目标）。
(3)由于 ρ∈(0,0.5) 且 g_k^Td_k<0 （ d_k 是一个下降方向的充要条件），故第2个式子右边比第1个式子右边要小，即：
α_k(1−ρ)g_k^Td_k<α_kρg_k^Td_k<0
如果步长 α 太小的话，会导致这个不等式接近于不成立的边缘。因此，式2就保证了 α 不能太小。

我还要把很多书中都用来描述Armijo-Goldstein准则的一幅图搬出来说明一下

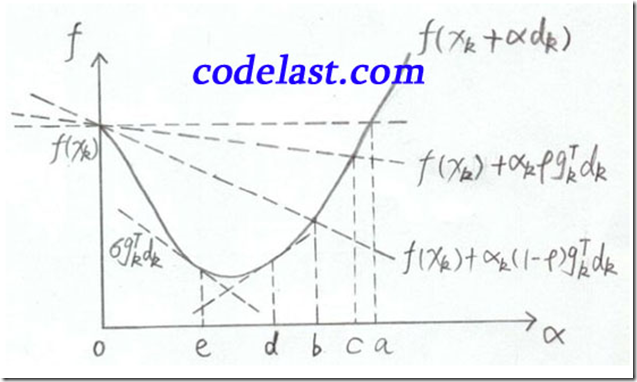
横坐标是 α ，纵坐标是 f ，表示在 x_k,d_k 均为常量、 α 为自变量变化的情况下，目标函数值随之变化的情况。
之所以说 x_k,d_k 均为常量，是因为在一维搜索中，在某一个确定的点 x_k 上，搜索方向 d_k 确定后，我们只需要找到一个合适的步长 α 就可以了。
当 x 为常量， α 为自变量时， f(x+αd) 可能是非线性函数（例如目标函数为 y=x2 时）。因此图中是一条曲线。
右上角的 f(x_k+αd_k) 并不是表示一个特定点的值，而是表示这条曲线是以 α 为自变量、 x_k,d_k 为常量的函数图形。
当 α=0 时，函数值为 f(x_k) ，如图中左上方所示。水平的那条虚线是函数值为 f(x_k) 的基线，用于与其他函数值对比。
f(x_k)+α_kρg_k^Td_k 那条线在 f(x_k) 下方（前面已经分析过了，因为 g_k^Tdk<0 ）， f(x_k)+α_k(1−ρ)g_k^Td_k 又在 f(x_k)+α_kρg_k^Td_k 的下方（前面也已经分析过了），所以Armijo-Goldstein准则可能会把极小值点（可接受的区间）判断在区间bc内。显而易见，区间bc是有可能把极小值排除在外的（极小值在区间ed内）。
所以，为了解决这个问题，Wolfe-Powell准则应运而生。

Wolfe-Powell准则

Wolfe-Powell准则也有两个数学表达式，其中，第一个表达式与Armijo-Goldstein准则的第1个式子相同，第二个表达式为

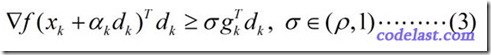
这个式子已经不是关于函数值的了，而是关于梯度的。
此式的几何解释为：可接受点处的切线斜率≥初始斜率的 σ 倍。
上面的图已经标出了 σg^T_kd_k 那条线（即 e 点处的切线），而初始点（ α=0 的点）处的切线是比 e 点处的切线要“斜”的，由于 σ∈(ρ,1) ，使得 e 点处的切线变得“不那么斜”了——不知道这种极为通俗而不够严谨的说法，是否有助于你理解。
这样做的结果就是，我们将极小值包含在了可接受的区间内（ e 点右边的区间）。

Wolfe-Powell准则到这里还没有结束！在某些书中，你会看到用另一个所谓的“更强的条件”来代替(3)式，即：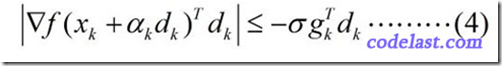

这个式子和(3)式相比，就是左边加了一个绝对值符号，右边换了一下正负号（因为 g^T_kdk<0 ，所以 −σg^T_kd_k>0 ）。
这样做的结果就是：可接受的区间被限制在了 [b,d] 内，如图：

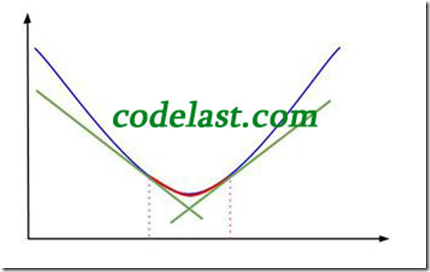
图中红线即为极小值被“夹击”的生动演示。

---

转自   https://www.codelast.com/