Jfinal极速开发微信系列教程（三）--------------对JSP的支持以及部署Tomcat运行异常问题

本文章主要解决以下问题：

• 1、Jfianl对JSP的支持2、Jfianl Maven项目部署到Tomcat，启动项目异常问题解决
• 
  第一个问题重现截图
  
  解决方案：
  1、在configConstant中添加视图的配置（默认支持的视图为freemarker）
  

  me.setViewType(ViewType.JSP);

  2、在Maven的配置文件中（pom.xml）添加lib 的支持

              <!-- jsp -->
          <dependency>
              <groupId>org.eclipse.jetty</groupId>
              <artifactId>jetty-jsp</artifactId>
              <version>8.1.8.v20121106</version>
              <scope>provided</scope>
          </dependency>
          <!-- jsp -->     

  第二个问题重现截图

  

  解决方案：
   点击项目右键属性properties>Deployment Assembly>add>Java Build Path Entries>Maven Dependencies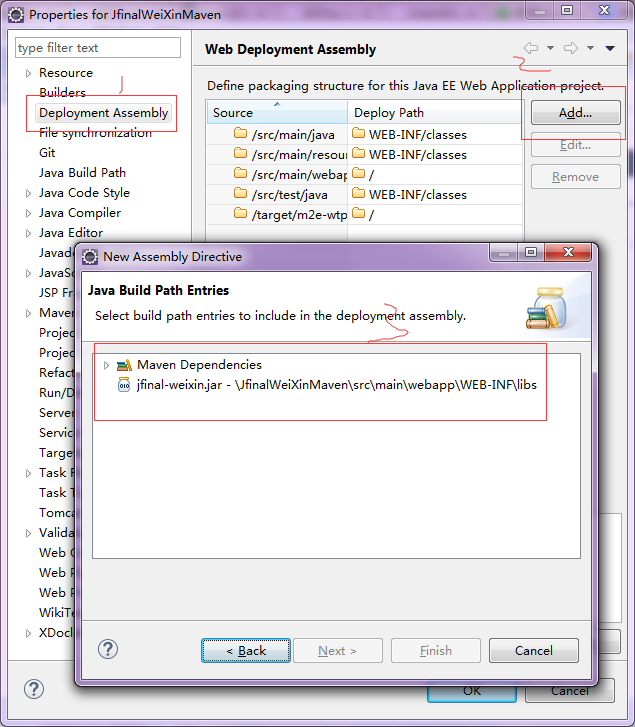 
  
  

　　

　　Jfianl 微信开发开源项目

       https://github.com/Javen205/jfinal_qyweixin.git  Jfianl极速开发企业公众号
    

　　https://github.com/Javen205/JfinalWeiXinMaven.git  Jfianl极速开发微信公众号 

　　　　

如果对你有帮助请我喝杯咖啡 左微信 右支付宝 个人微信公众号javenlife