协方差（Covariance）

统计学上用方差和标准差来度量数据的离散程度 ，但是方差和标准差是用来描述一维数据的（或者说是多维数据的一个维度），现实生活中我们常常会碰到多维数据，因此人们发明了协方差（covariance），用来度量两个随机变量之间的关系。

我们仿照方差的公式来定义协方差：

方差： 

协方差： 

（注：因为这里是计算样本的方差，因此用n-1。之所以除以n-1而不是除以n，是因为这样能使我们以较小的样本集更好地逼近总体，即统计上所谓的“无偏估计”。）

协方差如果为正值，说明两个变量的变化趋势一致；如果为负值， 说明两个变量的变化趋势相反；如果为0，则两个变量之间不相关（注：协方差为0不代表这两个变量相互独立。不相关是指两个随机变量之间没有近似的线性关系，而独立是指两个变量之间没有任何关系）。

但是协方差也只能处理二维问题，如果有n个变量X1、X2、···Xn，那怎么表示这些变量之间的关系呢？解决办法就是把它们两两之间的协方差组成协方差矩阵（covariance matrix）。

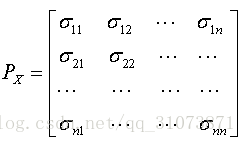
协方差矩阵是这样来定义的：

如果有n个变量：

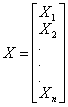
那么上述n个变量的协方差矩阵就是：

其中，