浅谈压缩感知(十五):感知矩阵之spark常数
在压缩感知中,有一些用来评价感知矩阵(非测量矩阵)的指标,如常见的RIP等,除了RIP之外,spark常数也能够用来衡量能否成为合适的感知矩阵。
0、相关概念与符号

1、零空间条件NULL Space Condition
在介绍spark之前,先考虑一下感知矩阵的零空间。
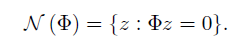
这里从矩阵的零空间来考虑测量矩阵需满足的条件:对于K稀疏的信号x,当且仅当测量矩阵的零空间与2K个基向量张成的线性空间没有交集,或者说零空间中的向量不在2K个基向量张成的线性空间中。
上述描述的性质似乎有点难懂,那么与之等价的表述就是spark常数。

2、spark常数定义
简单来说就是,矩阵列线性相关向量组的最小数目。(注意,这里的矩阵指的是感知矩阵,即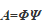 ,并非测量矩阵或稀疏基)
,并非测量矩阵或稀疏基)
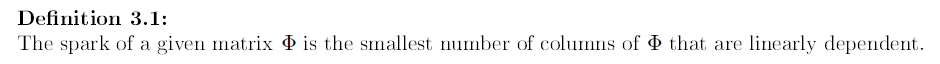
3、spark评价定理
当且仅当spark(Φ)>2k时,可以通过最小0范数优化问题得到k-稀疏信号x的精确近似。
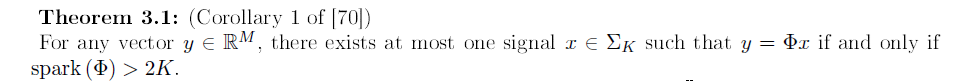
4、线性相关
定义:

定理:

性质:

5、定理证明
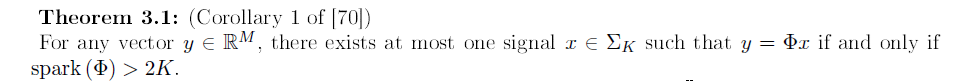
反证法。
第一步证明:对于任意的向量y,存在至多一个K稀疏的信号x,使得 ,则
,则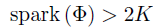 。
。
证明:假设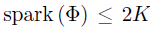 ,即根据定义感知矩阵的线性相关列小于或等于2K,从线性相关的定义出发,
,即根据定义感知矩阵的线性相关列小于或等于2K,从线性相关的定义出发,
存在某个向量 ,即
,即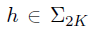 ,使得
,使得 且h不等于0。
且h不等于0。
由于 ,则h可以表示为:
,则h可以表示为: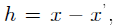
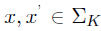 ,因此
,因此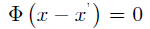
从而得到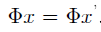 。
。
但是我们的条件中说明了至多只有一个K稀疏的信号x,因此与原条件矛盾,故假设不成立,原命题成立。
第二步证明:对于任意的向量y,满足 且
且 的K稀疏信号x至多有一个。
的K稀疏信号x至多有一个。
证明:假设K稀疏信号x至少有两个,设为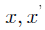 ,则
,则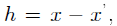
 。
。
因为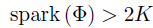 ,即根据定义感知矩阵的线性相关列大于2K,从线性相关的定义出发,
,即根据定义感知矩阵的线性相关列大于2K,从线性相关的定义出发,
存在某个向量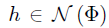 ,使得
,使得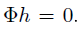 ,且h不等于0。而感知矩阵的零空间应该大于2K维,而假设中的h所在子空间小于或等于2K维,要满足
,且h不等于0。而感知矩阵的零空间应该大于2K维,而假设中的h所在子空间小于或等于2K维,要满足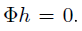 ,当且仅当h=0的时候,即
,当且仅当h=0的时候,即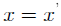 ,与原假设矛盾,因此假设不成立,原命题成立。
,与原假设矛盾,因此假设不成立,原命题成立。
6、spark常数与矩阵的秩
虽然spark与秩(rank)在某些方面很相似,但它们实际上是完全不同的,矩阵的秩是最大的线性无关的列数,而Spark是最小的线性相关的列数;有的时候矩阵满秩但spark=2。
还是通过例子理解吧:


浅谈压缩感知(十五):感知矩阵之spark常数的更多相关文章
- 浅谈压缩感知(二十):OMP与压缩感知
主要内容: OMP在稀疏分解与压缩感知中的异同 压缩感知通过OMP重构信号的唯一性 一.OMP在稀疏分解与压缩感知中的异同 .稀疏分解要解决的问题是在冗余字典(超完备字典)A中选出k列,用这k列的线性 ...
- 浅谈压缩感知(二十四):压缩感知重构算法之子空间追踪(SP)
主要内容: SP的算法流程 SP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 SP与CoSaMP的性能比较 一.SP的算法流程 压缩采样匹配追踪(CoSaMP)与子 ...
- 浅谈压缩感知(二十一):压缩感知重构算法之正交匹配追踪(OMP)
主要内容: OMP的算法流程 OMP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 稀疏度K与重构成功概率关系的实验与结果 一.OMP的算法流程 二.OMP的MATL ...
- []转帖] 浅谈Linux下的五种I/O模型
浅谈Linux下的五种I/O模型 https://www.cnblogs.com/chy2055/p/5220793.html 一.关于I/O模型的引出 我们都知道,为了OS的安全性等的考虑,进程是 ...
- 浅谈压缩感知(十六):感知矩阵之RIP
在压缩感知中,总是看到"矩阵满足RIP"之类的字眼,没错,这是一个压缩感知绕不开的术语,有限等距性质(Restricted Isometry Property, RIP). 注意: ...
- 【原创】浅谈指针(十二)关于static(上)
0.前言 这个系列基本上是一月一更到两月一更 今天写一篇关于static的,内含大量干货,做好准备 1.基础知识的回顾 1.1.内存的种类 一般来说,我们之前已经讲过的变量(或者说是内存)可以大体分为 ...
- 浅谈压缩感知(二十五):压缩感知重构算法之分段正交匹配追踪(StOMP)
主要内容: StOMP的算法流程 StOMP的MATLAB实现 一维信号的实验与结果 门限参数Ts.测量数M与重构成功概率关系的实验与结果 一.StOMP的算法流程 分段正交匹配追踪(Stagewis ...
- 浅谈压缩感知(十四):傅里叶矩阵与小波变换矩阵的MATLAB实现
主要内容: 傅里叶矩阵及其MATLAB实现 小波变换矩阵及其MATLAB实现 傅里叶矩阵及其MATLAB实现 傅里叶矩阵的定义:(来源: http://mathworld.wolfram.com/F ...
- 浅谈压缩感知(二十六):压缩感知重构算法之分段弱正交匹配追踪(SWOMP)
主要内容: SWOMP的算法流程 SWOMP的MATLAB实现 一维信号的实验与结果 门限参数a.测量数M与重构成功概率关系的实验与结果 SWOMP与StOMP性能比较 一.SWOMP的算法流程 分段 ...
随机推荐
- CRC32 of Ether FCS with STM32
Everyone knows that STM32F1xx, STM32F2xx, STM32F4xx have a hardware unit with a polynomial CRC32 0x0 ...
- [Go] defer 语句
Go 还有一些特有的流程控制语句,其中一个就是 defer 语句.该语句用于延迟调用指定的函数,它只能出现在函数的内部,由 defer 关键字以及针对某个函数的调用表达式组成.这里被调用的函数称为 延 ...
- 使用SIGALRM信号为阻塞操作设置超时
我们经常会遇到为阻塞操作设置超时的问题,比如说阻塞套接字read读取设置10秒超时,其中一个办法就是调用alarm函数,它在指定超时时期产生SIGALRM信号,使得阻塞操作中断. 但其弊端在于: 1. ...
- IE中div被视频遮住的解决方法
使用embed来内嵌视频,因为视频是windows media player,上面想用div浮动一些内容,之前尝试了一些方法,比如 1. 通过设定不同组件的z-index值 2. 通过设定 wmode ...
- Android:intent的基础
只有一个活动的应用也太简单了吧?没错,你的追求应该更高一点.不管你想创建多少 个活动,方法都和上一节中介绍的是一样的.唯一的问题在于,你在启动器中点击应用的图 标只会进入到该应用的主活动,那么怎样才能 ...
- NavigateToPageAction打开新页面
首先要加上两个命名空间 分别为: xmlns:i="clr-namespace:System.Windows.Interactivity;assembly=System.Windows.In ...
- C#编程(四十三)----------Lambda表达式
Lambda表达式 案例: using System; using System.Collections.Generic; using System.Linq; using System.Text; ...
- JasperReports+iReport在eclipse中的使用(转)
一.介绍 1)它可以PDF,HTML,XML等多种形式产生报表或动态报表,在新版本还支持CSV,XLS,RTF等格式的报表: 2)它按预定义的XML文档来组织数据,来源多(如:关系数据库,Java容器 ...
- Struts2 注解模式
相信大家一定看到了两个class中定义了一样的action,不过看类的元数据,是不同的命名空间.这里比较重要(对我来说)的是 @Action(value = "/login", r ...
- Android Studio 出现 Gradle's dependency cache may be corrupt 错误分析
http://blog.csdn.net/u014231734/article/details/41913775 情况说明: 之前下载了 Android Studio 1.0rc2候选版,那时候把 S ...
