主成分分析(PCA)算法,K-L变换 角度
主成分分析(PCA)是多元统计分析中用来分析数据的一种方法,它是用一种较少数 量的特征对样本进行描述以达到降低特征空间维数的方法,它的本质实际上是K-L变换。PCA方法最著名的应用应该是在人脸识别中特征提取及数据维,我们知 道输入200*200大小的人脸图像,单单提取它的灰度值作为原始特征,则这个原始特征将达到40000维,这给后面分类器的处理将带来极大的难度。著名 的人脸识别Eigenface算法就是采用PCA算法,用一个低维子空间描述人脸图像,同时用保存了识别所需要的信息。下面先介绍下PCA算法的本质K- L变换。
1、K-L变换(卡洛南-洛伊(Karhunen-Loeve)变换):最优正交变换
- 一种常用的特征提取方法;
- 最小均方误差意义下的最优正交变换;
- 在消除模式特征之间的相关性、突出差异性方面有最优的效果。
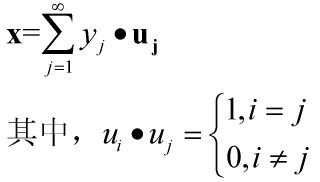


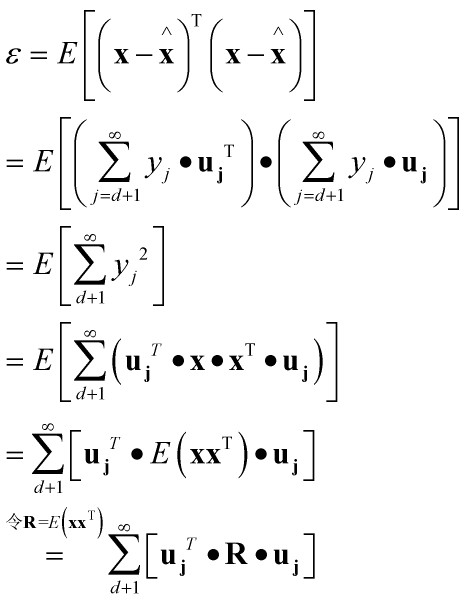


 取得最小值。
取得最小值。
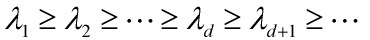



向量y就是变换(降维)后的系数向量,在人脸识别Eigenface算法中就是用系数向量y代替原始特征向量x进行识别。


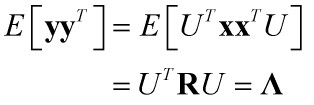
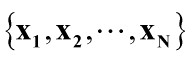 。
。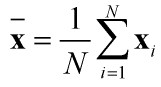
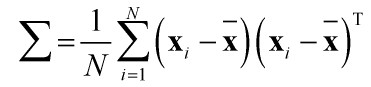
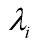 ,这些特征向量组成的矩阵U就是人脸空间的正交基底,用它们的线性组合可以重构出样本中任意的人脸图像,(如果有朋友不太理解这句话的意思,请看下面的总结2。)并且图像信息集中在特征值大的特征向量中,即使丢弃特征值小的向量也不会影响图像质量。
,这些特征向量组成的矩阵U就是人脸空间的正交基底,用它们的线性组合可以重构出样本中任意的人脸图像,(如果有朋友不太理解这句话的意思,请看下面的总结2。)并且图像信息集中在特征值大的特征向量中,即使丢弃特征值小的向量也不会影响图像质量。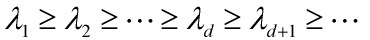 。由大于
。由大于 的
的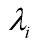 对应的特征向量构成主成分,主成分构成的变换矩阵为:
对应的特征向量构成主成分,主成分构成的变换矩阵为: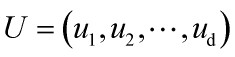
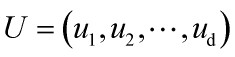 构成的特征脸子空间中,U的维数为M×d。有了这样一个降维的子空间,任何一幅人脸图像都可以向其作投影
构成的特征脸子空间中,U的维数为M×d。有了这样一个降维的子空间,任何一幅人脸图像都可以向其作投影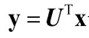 ,即并获得一组坐标系数,即低维向量y,维数d×1,为称为KL分解系数。这组系数表明了图像在子空间的位置,从而可以作为人脸识别的依据。
,即并获得一组坐标系数,即低维向量y,维数d×1,为称为KL分解系数。这组系数表明了图像在子空间的位置,从而可以作为人脸识别的依据。 的特征向量和特征值,这里怎么求的是协方差矩阵
的特征向量和特征值,这里怎么求的是协方差矩阵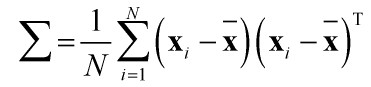 ?
?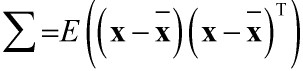 ,可以看出其实
,可以看出其实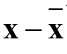 用代替x就成了相关矩阵R,相当于原始样本向量都减去个平均向量,实质上还是一样的,协方差矩阵也是实对称矩阵。
用代替x就成了相关矩阵R,相当于原始样本向量都减去个平均向量,实质上还是一样的,协方差矩阵也是实对称矩阵。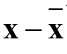 ,则
,则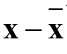 在特征脸空间U的投影,可以表示为系数向量y:
在特征脸空间U的投影,可以表示为系数向量y:
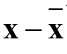 的维数为M×1,y的维数d×1。若M为200*200=40000维,取200个主成分,即200个特征向量,则最后投影的系数向量y维数降维200维。
的维数为M×1,y的维数d×1。若M为200*200=40000维,取200个主成分,即200个特征向量,则最后投影的系数向量y维数降维200维。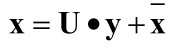
主成分分析(PCA)算法,K-L变换 角度的更多相关文章
- 机器学习--主成分分析(PCA)算法的原理及优缺点
一.PCA算法的原理 PCA(principle component analysis),即主成分分析法,是一个非监督的机器学习算法,是一种用于探索高维数据结构的技术,主要用于对数据的降维,通过降维可 ...
- Python的主成分分析PCA算法
这篇文章很不错:https://blog.csdn.net/u013082989/article/details/53792010 为什么数据处理之前要进行归一化???(这个一直不明白) 这个也很不错 ...
- 主成分分析 PCA算法原理
对同一个体进行多项观察时,必定涉及多个随机变量X1,X2,…,Xp,它们都是的相关性, 一时难以综合.这时就需要借助主成分分析 (principal component analysis)来概括诸多信 ...
- 一步步教你轻松学主成分分析PCA降维算法
一步步教你轻松学主成分分析PCA降维算法 (白宁超 2018年10月22日10:14:18) 摘要:主成分分析(英语:Principal components analysis,PCA)是一种分析.简 ...
- K-L变换和 主成分分析PCA
一.K-L变换 说PCA的话,必须先介绍一下K-L变换了. K-L变换是Karhunen-Loeve变换的简称,是一种特殊的正交变换.它是建立在统计特性基础上的一种变换,有的文献也称其为霍特林(Hot ...
- 机器学习 —— 基础整理(四)特征提取之线性方法:主成分分析PCA、独立成分分析ICA、线性判别分析LDA
本文简单整理了以下内容: (一)维数灾难 (二)特征提取--线性方法 1. 主成分分析PCA 2. 独立成分分析ICA 3. 线性判别分析LDA (一)维数灾难(Curse of dimensiona ...
- 模式识别(1)——PCA算法
作者:桂. 时间:2017-02-26 19:54:26 链接:http://www.cnblogs.com/xingshansi/articles/6445625.html 声明:转载请注明出处, ...
- 05-03 主成分分析(PCA)
目录 主成分分析(PCA) 一.维数灾难和降维 二.主成分分析学习目标 三.主成分分析详解 3.1 主成分分析两个条件 3.2 基于最近重构性推导PCA 3.2.1 主成分分析目标函数 3.2.2 主 ...
- 机器学习降维方法概括, LASSO参数缩减、主成分分析PCA、小波分析、线性判别LDA、拉普拉斯映射、深度学习SparseAutoEncoder、矩阵奇异值分解SVD、LLE局部线性嵌入、Isomap等距映射
机器学习降维方法概括 版权声明:本文为博主原创文章,未经博主允许不得转载. https://blog.csdn.net/u014772862/article/details/52335970 最近 ...
随机推荐
- jquery.peity.js简介
jQuery简单图表peity.js <html xmlns="http://www.w3.org/1999/xhtml"> <head> <titl ...
- 【转】java:Session(会话)机制详解
书中讲:以下情况,Session结束生命周期,Servlet容器将Session所占资源释放:1.客户端关闭浏览器2.Session过期3.服务器端调用了HttpSession的invalidate( ...
- Esper学习之十二:EPL语法(八)
今天的内容十分重要,在Esper的应用中是十分常用的功能之一.它是一种事件集合,我们可以对这个集合进行增删查改,所以在复杂的业务场景中我们肯定不会缺少它.它就是Named Window. 由于本篇篇幅 ...
- android 线程间的通信
(转自:http://www.cnblogs.com/allin/archive/2010/05/19/1738800.html) andriod提供了 Handler 和 Looper 来满足线程间 ...
- $@和 $*-linux_Shell
=================1.问题======= 在使用$@和 $*的时候有时候会混淆. ================2.实践出真知===== 分别用三种参数设置: "a b c ...
- rpmdb: unable to join the environment的问题解决
今天笔者在Centos 6.3上使用yum安装lsof软件时,报如下错误: [root@ ~]# yum install lsof -y rpmdb: unable to join the envir ...
- adviser vs mentor
研究生或博士生提到自己导师的时候是说adviser呢?还是mentor呢? 至少我认识一个Berkeley的博士是说adviser的. 另外,我的导师也是说adviser. 那还是说adviser吧- ...
- SDWebImage第三方库使用注意的一些问题
1.利用"UIImageView+WebCache.h"加载图片数据 例如: UIImage *placeHolderImg = [UIImage imageNamed:@&quo ...
- ubuntu16.04下安装ros-kinetic
参考:http://wiki.ros.org/kinetic/Installation/Ubuntu 1.添加ROS软件源 ~$ sudo sh -c 'echo "deb http://p ...
- .Net Identity OAuth 2.0 SecurityStamp 使用
起源: 近期帮别人做项目,涉及到OAuth认证,服务端主动使token失效,要使对应用户不能再继续访问,只能重新登陆,或者重新授权. 场景: 这种场景OAuth2.0是支持的,比如用户修改了密码,那所 ...
