BZOJ 1006: [HNOI2008]神奇的国度（弦图染色）

http://www.lydsy.com/JudgeOnline/problem.php?id=1006

题意：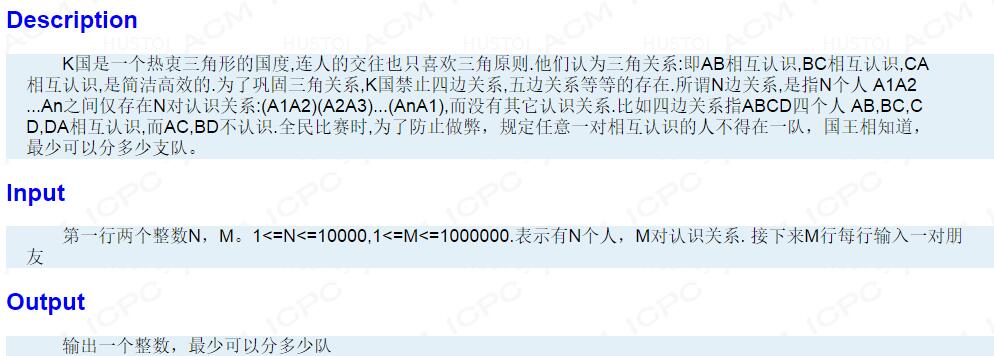

思路：

这个就是弦图染色问题，弦图啥的反正我也不懂，具体看论文https://wenku.baidu.com/view/07f4be196c175f0e7cd13784.html

这里的话就是用最大势算法求了一个完美消除序列，然后根据完美消除序列来进行染色即可。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,ll> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 int n, m;
 int head[maxn];
 int tot;
 int ans;
 int label[maxn]; //label[i]表示第i个点与多少个已标号的点相邻，每次选择label[i]最大的未标号的点进行标号
 int vis[maxn];
 int q[maxn];
 int check[maxn];
 int col[maxn];

 struct node
 {
     int v;
     int next;
 }e[*+];

 void addEdge(int u, int v)
 {
     e[tot].v=v;
     e[tot].next=head[u];
     head[u]=tot++;
 }

 void MCS()  //最大势算法求完美消除序列
 {
     memset(vis,,sizeof(vis));
     for(int i=n;i;i--)
     {
         int pos=;
         for(int j=;j<=n;j++)   //选择当前未访问且label值最大的
             if(!vis[j] && label[j]>=label[pos])   pos=j;
         vis[pos]=;
         q[i]=pos;
         for(int j=head[pos];j!=-;j=e[j].next)  //与pos结点相邻的结点label值+1
             label[e[j].v]++;
     }
 }

 void color()//染色
 {
     memset(check,,sizeof(check));
     memset(col,,sizeof(col));
     for(int i=n;i;i--)
     {
         int pos=q[i],j;
         for(int j=head[pos];j!=-;j=e[j].next)  check[col[e[j].v]]=i;
         for(j=;;j++)  if(check[j]!=i)  break;
         col[pos]=j;
         if(j>ans)  ans=j;
     }
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n,&m))
     {
         tot=;
         memset(head,-,sizeof(head));
         while(m--)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             addEdge(u,v);
             addEdge(v,u);
         }
         ans=;
         MCS();
         color();
         printf("%d\n",ans);
     }
     return ;
 }