POJ - 2528Mayor's posters （离散化+线段树区间覆盖）

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:

• Every candidate can place exactly one poster on the wall.
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
• The wall is divided into segments and the width of each segment is one byte.
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.

Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l
_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l
_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l
_i, l
_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed.

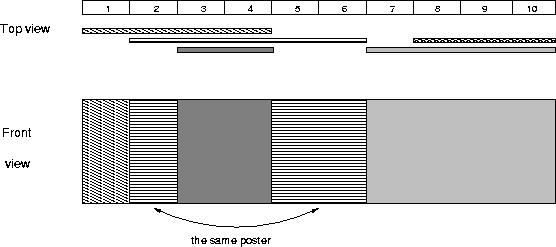
The picture below illustrates the case of the sample input.

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

这道题我是参考大佬博客的，一开始我对这道题完全不知道怎么下手，百度了一下，发现是用离散化＋线段树，其实我一开始还不知离散化是什么，又去学习了离散化再来写这道题；

下面是博主的分析：

题意：贴海报，海报可以覆盖，会给出你每张海报的长款，然后问你最后还能看到几张海报。

我做这道题遇到的坑点，第一点离散化，第二点线段树用的不熟练

解法：离散化，如下面的例子（题目的样例），因为单位1是一个单位长度，将下面的

1   2   3   4  6   7   8   10

—  —  —  —  —  —  —  —

1   2   3   4  5   6   7   8

离散化  X[1] = 1; X[2] = 2; X[3] = 3; X[4] = 4; X[5] = 6; X[6] = 7; X[7] = 8,X[8] = 10;

于是将一个很大的区间映射到一个较小的区间之中了，然后再对每一张海报依次更新在宽度为1~8的墙上(用线段树），

最后统计不同颜色的段数。但是只是这样简单的离散化是错误的，

如三张海报为：1~10 1~4 6~10离散化时 X[ 1 ] = 1, X[ 2 ] = 4, X[ 3 ] = 6, X[ 4 ] = 10

第一张海报时：墙的1~4被染为1；

第二张海报时：墙的1~2被染为2，3~4仍为1

；第三张海报时：墙的3~4被染为3，1~2仍为2。

最终，第一张海报就显示被完全覆盖了，于是输出2，但实际上明显不是这样，正确输出为3。

新的离散方法为：在相差大于1的数间加一个数，例如在上面1 4 6 10中间加5（算法中实际上1，4之间，6，10之间都新增了数的）

X[ 1 ] = 1, X[ 2 ] = 4, X[ 3 ] = 5, X[ 4 ] = 6， X[ 5 ] = 10

这样之后，第一次是1~5被染成1；第二次1~2被染成2；第三次4~5被染成3最终，1~2为2，3为1，4~5为3，于是输出正确结果3。

代码如下：

 #include<iostream>
 #include<stdio.h>
 #include<algorithm>
 #include<string.h>
 using namespace std;

 const int MAXN = ;
 int T;
 int N;
 int x[MAXN] , y[MAXN];
 int lisan[MAXN*];
 bool vis[MAXN*];
 int tree[MAXN*];   //离散化要开16倍空间
 int size ;
 int num = ;
 int tmp;
 int ans ;
 void pushdown(int rt )
 {
     tree[rt*] = tree[rt];
     tree[rt*+] = tree[rt];
     tree[rt] = ;
 }
 void Update(int tpx ,int tpy ,int value, int l ,int r ,int rt)
 {
     if(l>=tpx&&r<=tpy)
     {
         tree[rt] = value;
         return;
     }
     if(tree[rt]!=)
     pushdown(rt);
     int m = (l+r)/;

     if(tpx<=m)
     {
         Update(tpx,tpy,value,l,m,rt*);
     }
     if(tpy>m)
     {
         Update(tpx,tpy,value,m+,r,rt*+);
     }

 }
 void Query(int l ,int r ,int rt)
 {
     if(tree[rt]!=)
     {
         if(!vis[tree[rt]])
         {
             ans++;
             vis[tree[rt]] = ;
         }
         return ;
     }
     if(l==r)
     return;
     if(tree[rt]!=)
     {
         pushdown(rt);
     }
     int m = (l+r)/;
     Query(l,m,rt*);
     Query(m+,r,rt*+);
 }

 int main()
 {
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&N);
         num = ;
         memset(tree,,sizeof(tree));
         memset(vis,,sizeof(vis));
         for(int i =  ; i <= N ;i++)
         {
             scanf("%d%d",&x[i],&y[i]);
              lisan[num++] = x[i];
              lisan[num++] = y[i];
         }
         sort(lisan,lisan+num);    //排序后离散化
         size = unique(lisan,lisan+num)-lisan;   //获得离散化后的长度
         tmp = size;
         for(int i =  ; i < tmp ;i++)
         {
             if(lisan[i]-lisan[i-]>)    //这样离散化才正确；见上面分析；
             {
                 lisan[size++] = lisan[i-] + ;
             }
         }
         sort(lisan,lisan+size);  //再排序一次
         for(int i =  ; i <= N ;i++ )
         {
             int tpx = lower_bound(lisan,lisan+size,x[i])-lisan;//获取位置
             int tpy = lower_bound(lisan,lisan+size,y[i])-lisan;
             Update(tpx,tpy,i,,size-,);
         }
         ans =  ;
         Query(,size-,);
         printf("%d\n",ans);
     }
     return ;
 }