Erlang C 與M/M/N排隊模型
一何谓排队模型
在现实生活中排队的现象可说是无处不在,如:买票、超商、百货公司…等。顾客总是在揣测"排在哪一个服务台会比较快?"或"到底还要排多久呢?"类似这样的问题;相对的,由经营者的立场也在思考在什么时间点要开设几个服务窗口才能降低成本且达到最大的效益。为了探讨这类问题,数学家们逐渐发展出了名为"排队理论(Queuing theory)"的工具。排队理论主要是利用机率的假设做为分析条件,顾名思义是一套研究排队等候时间问题的工具。排队理论由丹麦的学者Erlang在1910年左右首先提出来的,起初是为了解决电话网路中顾客等候时间的问题,接着由俄国数学家Markov建立了所谓的马可夫模型(Markov Model)。而Kendall在1953年提出了A/B/C/X/Y/Z表示法,其中
|
A |
顾客进入系统中所服从的机率分配模型。 (如:来电量) |
|
B |
服务时间长短所服从的机率分配模型。 (如:通话时间) |
|
C |
服务台的个数。 (如:座席数) |
|
X |
平行队列的数目。 |
|
Y |
系统最大容量。 |
|
Z |
意指排队纪律,通常有FCFS先到先服务、LCFS后来服务与RSS随机服务等型式。 |
将排队理论复杂的假设以简单明确的方式表示。排队理论发展至今,已被广泛应用在网路通讯、生产、运输和库存等各项资源共享的随机服务系统。而Erlang C与M/M/N排队模型是具有相同的假设,如下
(1) 顾客到达服从参数为的Poisson随机过程。 (M)
(2) 服务时间服从参数为的指数机率分配。 (M)
(3) 服务台个数为N个。 (N)
(4) 平行对列数目为1。
(5) 系统最大容量无限多个顾客在系统中。
(6) FCFS先来先服务。
二参数定义与公式
|
参数 |
定义 |
公式与实例 (座席数=25位) (每15分钟来电量=100通) (平均处理时间=180秒) |
|
|
每单位时间顾客到达率 |
|
|
|
每单位时间的服务率 |
|
|
|
系统负载率, |
|
|
|
无顾客在系统中的机率 |
|
|
|
顾客必须等候的机率 |
|
|
|
期望排队长度 |
|
|
|
期望排队等候时间 |
|
|
|
服务水准(Sever Level),在t秒内接起的机率 |
|
Erlang C 與M/M/N排隊模型的更多相关文章
- Linux Kernel 排程機制介紹
http://loda.hala01.com/2011/12/linux-kernel-%E6%8E%92%E7%A8%8B%E6%A9%9F%E5%88%B6%E4%BB%8B%E7%B4%B9/ ...
- 易普优APS-3C行业解决方案助力国家智能制造示范车间实现高效计划排程
一. 项目背景 广东劲胜智能集团国家智能制造专项——移动终端金属加工智能制造新模式项目是2015年国家94家智能制1.造专项之一.本项目实施车间为金属CNC加工车间(下称“智能制造示范车间” ...
- 使用WebClient與HttpWebRequest的差異
在<Windows Phone 7-下載檔案至Isolated Storage>提到了透過WebClient的功能將網站上的檔案下載至 WP7的Isoated Storage之中.但實際的 ...
- 【案例】大型摩托制造企业如何高效排产?看APS系统如何帮忙
江门市大长江集团有限公司(下文简称,大长江集团)创建于1991年11月,是豪爵控股下属子公司. 大长江生产计划管理从最初的电子表格Excel 公式辅助计算,发展到按公司业务需求,利用Excel VBA ...
- 为什么众多软件厂商无法提供APS高级计划排程系统?工厂目前生产计划是怎么排产的?
一.行业现状如想了解一下目前现状,去考察一下上了ERP的企业,会发现一个有趣的现象该企业无论ERP软件搞得如何如火如荼,似乎都与生产调度人员无关. 车间里或者生产线上的生产作业计划.生产过程的调度和管 ...
- Cen0S下挂载设备
在CentOS中,如果我们要查看光驱,U盘或者要把安装包挂载到某个文件夹,我写下我的一些理解. 所谓的挂载,就是把物理设备或者文件(包含安装文件,压缩包等等),与系统中的某个目录建立一个快捷方式,然后 ...
- CAN
CAN Introduction Features Network Topology(CANbus網路架構) MESSAGE TRANSFER(CAN通訊的資料格式) 1.DATA FRAME(資料通 ...
- Linux根目录详解-转自鸟哥的私房菜
转自:http://myhat.blog.51cto.com/391263/107931/ *根目录(/)的意义与内容: 根目录是整个系统最重要的一个目录,因为不但所有的目录都是由根目录衍生出来的 ...
- BT觀念分享和常見問題彙整
一. TCP/IP基本觀念 1. IP : 每台在TCP/IP網路上的電腦必須具備的一個代表號或一個地址.IP又分為private IP(192.168.x.x /10.x.x.x /172.16.x ...
随机推荐
- Dapper相关了解
公司新项目用的是Dapper,做的时候没有具体看dapper的具体用法,现在回来回顾总结一下. 1-总体介绍dapper 我们都知道ORM全称叫做Object Relationship Mapper, ...
- Django之博客系统:增加评论
3既然是博客,那肯定就有留言评论系统.在这一章就来建立一个评论系统. 1 创建一个模型来保存评论 2 创建一个表单来提交评论并且验证输入的数据 3 添加一个视图函数来处理表单和保存新的评论到数据库 4 ...
- (Delphi)第一个Windows 32 API的窗口程序
program Project1; uses Winapi.Windows, Winapi.messages; {$R *.res} const className = 'MyDelphiWindow ...
- ubuntu - 14.04,必须会的技能-安装PPA源中的程序,更大范围使用deb格式安装文件!!
在使用ubuntu时候,管理各种软件最方便的方式肯定是使用软件中心了,这个管理工具类似windows的 程序管理了,使用它有两个好处: 1,无需处理包依赖,linux里面程序存在各种依赖关系,这在以往 ...
- ios配置xmpp即时聊天-服务器端
一.安装 到MySQL官网上http://dev.mysql.com/downloads/mysql/,下载mysql可安装dmg版本 比如:Mac OS X ver. 10.7 (x86, 64-b ...
- 【洛谷2324】[SCOI2005]骑士精神 IDA*
[SCOI2005]骑士精神 描述 在一个\(5×5\)的棋盘上有\(12\)个白色的骑士和\(12\)个黑色的骑士, 且有一个空位.在任何时候一个骑士都能按照骑 士的走法(它可以走到和它横坐标相差为 ...
- EXPEDI - Expedition 优先队列
题目描述 A group of cows grabbed a truck and ventured on an expedition deep into the jungle. Being rathe ...
- 树莓派编译安装 EMQ 服务器
前言 EMQ 是一款开源的物联网 MQTT 消息服务器,使用 Erlang/OTP 语言平台设计,在 DIY 智能家居时可以作为网关,前几天摸索了一下在树莓派中安装 EMQ 的方法,记录一下. 步骤 ...
- js 时间日期大小对比
var oDate1 = new Date(); var oDate2 = new Date("2019/01/07 10:00:00"); if (oDate1.getTime( ...
- django 母版与继承
在子页面的页面最上方使用下面的语法来继承母版. {% extends 'layouts.html' %} 块: 通过在母版中使用{% block xxx %}来定义块.在子页面中通过定义母版中的blo ...













 人
人
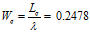 秒
秒
