poj 2486 树形DP n选m连续路径

题目连接：http://acm.hust.edu.cn/vjudge/problem/18071

资料连接：

http://blog.csdn.net/woshi250hua/article/details/7648798

http://blog.csdn.net/libin56842/article/details/10101807

这道题思路是这样的。

以这张图为例，以往的n选m题目，只要根节点选了，子树可以直接选，没有代价。所以可以直接dp[fa][j] = max(dp[fa][j],dp[fa][j-k]+dp[son][k])

但这题不一样，选了AB不代表你可以直接选C，需要按照一定的路径来，所以上面的就不适用了。那么这个问题如何解决？

我们可以这样想，就拿上图来说，以A点为研究对象时可以走的路有哪些情况

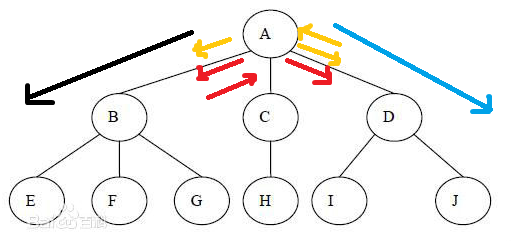
有四种：往左，往右，往左转一圈回来往右，往右转一圈回来往左

这四种情况其实包含两类动作，一类是往下搜索，一类是往下搜索然后回到原点。

这样状态就出来了，比起原本的我们要加一个状态，要记录回到原点的状态

dp[rt][j][0]表示回到原点，dp[son][j][1]表示不回原点

状态转移方程：

先维护回原点的状态

dp[rt][j][0] = max(dp[rt][j][0],dp[rt][j-k][0]+dp[son][k-2][0])

再分别维护左边回原点到右边

dp[rt][j][1] = max(dp[rt][j][1],dp[rt][j-k][0]+dp[son][k-1][1])

右边回原点到左边

dp[rt][j][1] = max(dp[rt][j][1],dp[rt][j-k][1]+dp[son][k-2][0])

#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std;

#define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 200+5
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f

int n,m;

struct node{int y,val,next;}tree[MAXN<<];

int head[MAXN],vis[MAXN],ptr=,val[MAXN],dp[MAXN][MAXN][];

void init()
{
    mem(head,-);
    mem(vis,);
    mem(dp,);
    ptr=;
}
void add(int x,int y)
{
    tree[ptr].y = y;
    tree[ptr].next = head[x];
    head[x] = ptr++;
}

void dfs(int rt)
{
    vis[rt]=;
    for(int i=;i<=m;i++) dp[rt][i][] = dp[rt][i][] = val[rt];
    for(int i = head[rt];i!=-;i=tree[i].next)
    {
        int y = tree[i].y;
        if(vis[y]) continue;
        dfs(y);

        //pf("y%d\n",y);
        for(int j=m;j>=;j--)
        {
            for(int k=;k<=j;k++)
            {
                dp[rt][j+][] = max(dp[rt][j+][],dp[rt][j-k][]+dp[y][k][]);
                dp[rt][j+][] = max(dp[rt][j+][],dp[rt][j-k][]+dp[y][k][]);
                dp[rt][j+][] = max(dp[rt][j+][],dp[rt][j-k][]+dp[y][k][]);
                //pf("v%d %d %d %d %d\n",j+2,k,dp[rt][j+2][0],dp[rt][j+2][1],dp[rt][j+1][1]);
            }
        }
    }
}

int main()
{
    int i,j,k;
    while(~sf("%d%d",&n,&m))
    {
        init();
        for(i=;i<=n;i++) sf("%d",&val[i]);

        for(i=;i<n;i++)
        {
            int x,y;
            sf("%d%d",&x,&y);
            add(x,y);
            add(y,x);
        }
        dfs();
        pf("%d\n",dp[][m][]);
    }
}
/*
7 5
0 5 7 2 15 9 10
1 2
1 3
2 4
2 5
3 6
3 7
*/