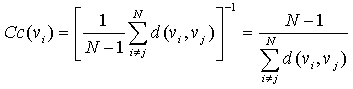PTA 7-12(图) 社交网络图中结点的“重要性”计算 最短路
7-12(图) 社交网络图中结点的“重要性”计算 (30 分)
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi的“紧密度中心性”Cc(vi)数学上定义为vi到其余所有结点vj (j≠i) 的最短距离d(vi,vj)的平均值的倒数:
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(≤104)是图中结点个数,顺便假设结点从1到N编号;M(≤105)是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤100)以及K个结点编号,用空格分隔。
输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35思路:简单的稀疏图最短路问题,甚至不需要保存边权(均为一),dijkstra算法裸过,读入的时候判一下是不是连通图
AC代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <cstdio>
#include <malloc.h> #define INF 0x3f3f3f3f
#define FRER() freopen("in.txt", "r", stdin)
#define FREW() freopen("out.txt", "w", stdout) using namespace std; const int maxn = + ; vector<int> g[maxn]; int n, m, s, u, v, vis[maxn], dis[maxn]; typedef pair<int, int> P; void dijkstra() {
memset(vis, , sizeof(vis));
memset(dis, INF, sizeof(dis));
priority_queue<P, vector<P>, greater<P> > q;
dis[s] = ;
q.push(make_pair(, s));
P tmp;
while(!q.empty()) {
tmp = q.top(); q.pop();
if(vis[tmp.second]) continue;
vis[tmp.second] = ;
for(int i = ; i < g[tmp.second].size(); ++i) {
if(tmp.first + < dis[g[tmp.second][i]]) {
dis[g[tmp.second][i]] = tmp.first + ;
q.push(make_pair(dis[g[tmp.second][i]], g[tmp.second][i]));
}
}
}
} double cal() {
double ans = ;
for(int i = ; i <= n; ++i)
ans += (double)dis[i];
return (n - ) / ans;
} int main()
{
scanf("%d %d", &n, &m);
int num = ;
while(m--) {
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
if(!vis[u]) vis[u] = , ++num;
if(!vis[v]) vis[v] = , ++num;
} bool ok = !(num == n);
scanf("%d", &m);
while(m--) {
scanf("%d", &s);
if(ok) printf("Cc(%d)=0.00\n", s);
else {
dijkstra();
printf("Cc(%d)=%.2lf\n", s, cal());
}
}
return ;
}
PTA 7-12(图) 社交网络图中结点的“重要性”计算 最短路的更多相关文章
- PTA 社交网络图中结点的“重要性”计算(30 分)
7-12 社交网络图中结点的“重要性”计算(30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互 ...
- PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分)
PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分) 7-36 社交网络图中结点的“重要性”计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某 ...
- 7-10 社交网络图中结点的“重要性”计算(30 point(s)) 【并查集+BFS】
7-10 社交网络图中结点的"重要性"计算(30 point(s)) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络 ...
- 社交网络图中结点的“重要性”计算 (30 分) C++解法
社交网络图中结点的"重要性"计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓 ...
- 7-11 社交网络图中结点的“重要性”计算 (30 分)(Dijkstra算法)
题意: 思路:对每个输入的点跑一遍dijkstra算法,然后对这个点到所有点的距离求和按公式输出就可以了. (这次尝试了用数组模拟链表来做最短路问题,刷新了自己对最短路的理解) 这里构造链表的过程我 ...
- dgraph解决社交关系中的正反向查找
dgraph解决社交关系中的正反向查找 本篇介绍的是, 社交关系中的关注者与被关注者在dgraph中如何实现查找. 对dgraph的基本操作不太清楚的可以看看我之前写的博客 dgraph实现基本操作 ...
- 全世界最详细的图形化VMware中linux环境下oracle安装(二)【weber出品必属精品】
<ORACLE 10.2.05版本的升级补丁安装> 首先我们解压 $ unzip p8202632_10205_LINUX.zip 解压后我们会发现多出了个文件夹,他是:Disk1,进入D ...
- 全世界最详细的图形化VMware中linux环境下oracle安装(一)【weber出品必属精品】
安装流程:前期准备工作--->安装ORACLE软件--->安装升级补丁--->安装odbc创建数据库--->安装监听器--->安装EM <前期准备工作> 安装 ...
- 【转】一张图解析FastAdmin中的表格列表的功能
一张图解析FastAdmin中的表格列表的功能 功能描述请根据图片上的数字索引查看对应功能说明. 1.时间筛选器如果想在搜索栏使用时间区间进行搜索,则可以在JS中修改修改字段属性,如 {field: ...
随机推荐
- Refactoring in Coding
Make changes on existing code for subsequent and constant changes of requirement. Reference:http://w ...
- WebAPI示例
一.新建项目 二. 代码: Models.Products实体类 public class Product { /// <summary> /// 产品编号 /// </summar ...
- lucene查询解析器语法
注意:使用QueryParser查询,关键词是会被分词的,如果不需要分词,可以选择使用Lucene提供的API查询类. Lucene提供了丰富的API来组合定制你所需要的查询器,同时也可以利用Quer ...
- C#实现屏幕指定区域截屏
//string Opath = @"C:/Picture"; //if (Opath.Substring(Opath.Length - 1, 1) != @ ...
- HTML-JS-CSS基础
HTML-JS-CSS基础 1.html hyper text markup language,超文本标记语言,所见即所得.web开发中用于展示功能的部分,浏览器可对其进行渲染.产生各种可视化组件,比 ...
- des的根据key进行加密和解密方法
DES加密: public static string DESEncode(string content, string key) { DESCryptoServiceProvider des = n ...
- javascript 时间格式化方法
对jquery进行扩展的方法: //对时间格式化(jquery方法扩展) Date.prototype.Format = function (fmt) { //author: meizz var o ...
- Python动态类型简单介绍
动态类型以及它提供的多态性,无疑是Python语言简洁性和灵活性的基础. 一.变量 <1>变量创建 一个变量a.当代码第一次给它赋值时就创建了它,之后的赋值将会改变已创建的变量名的值. ...
- Notepad++插件Emmet和Python Script的安装
最近在做一个项目,涉及到大量的HTML.CSS代码的编写,手动写代码效率实在 是低下.于是想搜索一下,有没有Notepad++插件可以支持自动生成的,果不其然还真有.Emmet,这款神器其实就是 Ze ...
- 多线程, Thread类,Runnable接口
多线程 线程:线程是进程中的一个执行单元,负责当前进程中程序的执行,一个进程中至少有一个线程.一个进程中是可以有多个线程的,这个应用程序也可以称之为多线程程序. 单线程程序:即,若有多个任务只能依次执 ...