bzoj2441 [中山市选2011]小W的问题(debug中)

2441: [中山市选2011]小W的问题

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 487  Solved: 186
[Submit][Status][Discuss]

Description

有一天，小W找了一个笛卡尔坐标系，并在上面选取了N个整点。他发现通过这些整点能够画出很多个“W”出来。具体来说，对于五个不同的点(x1, y1), (x2, y2), (x3, y3), (x4, y4), (x5, y5)，如果满足：

·x1 < x2 < x3 < x4 < x5

·y1 > y3 > y2

·y5 > y3 > y4

则称它们构成一个“W”形。

现在，小W想统计“W”形的个数，也就是满足上面条件的五元点组个数。你能帮助他吗？

。

Input

第一行包含一个整数N，表示点的个数。

下面N行每行两个整数，第i+1行为(xi, yi)，表示第i个点的坐标。

Output

仅包含一行，为“W”形个数模1 000 000 007的值。

Sample Input

6

1 10

2 1

3 5

4 6

5 1

6 10

Sample Output

3

HINT

对于100%的数据满足N ≤ 200 000，0 ≤ xi ≤ 10^9，0 ≤ yi ≤ 10^9

Source

Day2

开始做这道题的时候还是正中午，现在......

这题真的是烦，如果横纵坐标不相等，还好点，现在相等了，直接gg.

两个思路，一是统计下面几种图形的数量：

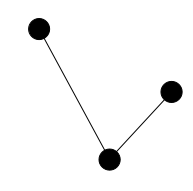
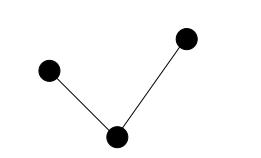
，容斥一下就好了.我写了横纵坐标不相等的代码，但是一旦横纵坐标相等就gg.

另外的思路是借鉴的网上其他题解的.

结果两份代码都没debug成功QAQ,省选前我会回来填坑的.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const ll maxn = ,mod = ,inf = ;

struct node
{
    ll x,y,x2,id;
}e[maxn];

int n;
ll ans1[maxn],ans2[maxn],b[maxn],sum[maxn << ],L[maxn << ],R[maxn << ],tag[maxn << ],ans,tot;

bool cmp(node a,node b)
{
    return a.y < b.y;
}

bool cmp2(node a,node b)
{
    return a.x < b.x;
}

void pushup(int o)
{
    sum[o] = sum[o * ] + sum[o *  + ];
    sum[o] %= mod;
}

void build(int o,int l,int r)
{
    L[o] = l,R[o] = r;
    sum[o] = tag[o] = ;
    if (l == r)
        return;
    int mid = (l + r) >> ;
    build(o * ,l,mid);
    build(o *  + ,mid + ,r);
    pushup(o);
}

void pushdown(int o)
{
    if (tag[o])
    {
        tag[o * ] += tag[o];
        tag[o * ] %= mod;
        tag[o *  + ] += tag[o];
        tag[o *  + ] %= mod;
        sum[o * ] += tag[o] * (R[o * ] - L[o * ] + ) % mod;
        sum[o *  + ] += tag[o] * (R[o *  + ] - L[o *  + ] + ) % mod;
        tag[o] = ;
    }
}

void update(int o,int l,int r,int x,int y,int v)
{
    if (x > y)
        return;
    if (x <= l && r <= y)
    {
        sum[o] += (r - l + ) * 1LL * v % mod;
        sum[o] %= mod;
        tag[o] += v;
        tag[o] %= mod;
        return;
    }
    pushdown(o);
    int mid = (l + r) >> ;
    if (x <= mid)
        update(o * ,l,mid,x,y,v);
    if (y > mid)
        update(o *  + ,mid + ,r,x,y,v);
    pushup(o);
}

void update2(int o,int l,int r,int pos,int v)
{
    if (l == r)
    {
        //sum[o] += v;
        //sum[o] %= mod;
        //tag[o] += v;
        //tag[o] %= mod;
        sum[o] = v;
        return;
    }
    pushdown(o);
    int mid = (l + r) >> ;
    if (pos <= mid)
        update2(o * ,l,mid,pos,v);
    else
        update2(o *  + ,mid + ,r,pos,v);
    pushup(o);
}

ll query(int o,int l,int r,int x,int y)
{
    if (x > y)
        return ;
    if (x <= l && r <= y)
        return sum[o];
    pushdown(o);
    ll res = ;
    int mid = (l + r) >> ;
    if (x <= mid)
        res += query(o * ,l,mid,x,y);
    res %= mod;
    if (y > mid)
        res += query(o *  + ,mid + ,r,x,y);
    res %= mod;
    return res;
}

void solve1()
{
    build(,,n);
    for (int i = ; i <= n; i++)
    {
        int j = i;
        while (j < n && e[i].y == e[j + ].y)
            j++;
        for (int k = i; k <= j; k++)
            update(,,n,e[k].x2,n,-);
        for (int k = i; k <= j; k++)
            ans1[e[k].id] = query(,,n,,e[k].x - );
        for (int k = i; k <= j; k++)
            update2(,,n,e[k].id,e[k].x - );
        i = j;
    }
}

void solve2()
{
    build(,,n);
    for (int i = ; i <= n; i++)
    {
        int j = i;
        while (j < n && e[i].y == e[j + ].y)
            j++;
        for (int k = i; k <= j; k++)
            update(,,n,,e[k].x - ,-);
        for (int k = i; k <= j; k++)
            ans2[e[k].id] = query(,,n,e[k].x2,n);
        for (int k = i; k <= j; k++)
            update2(,,n,e[k].id,n - e[k].x2 + );
        i = j;
    }
}

int main()
{
    scanf("%d",&n);
    for (int i = ; i <= n; i++)
    {
        scanf("%lld%lld",&e[i].x,&e[i].y);
        b[++tot] = e[i].x;
    }
    b[++tot] = inf;
    sort(b + ,b +  + tot);
    sort(e + ,e +  + n,cmp2);
    for (int i = ; i <= n; i++)
    {
        e[i].x2 = upper_bound(b + ,b +  + tot,e[i].x) - b;
        e[i].x = lower_bound(b + ,b +  + tot,e[i].x) - b;
        e[i].id = i;
    }
    sort(e + ,e +  + n,cmp);
    solve1();
    sort(e + ,e +  + n,cmp);
    solve2();
    /*
    for (int i = 1; i <= n; i++)
    {
        printf("%lld %lld\n",ans1[i],ans2[i]);
        ans += ans1[i] * ans2[i] % mod;
        ans %= mod;
    }
    */
    printf("%lld\n",ans);

    return ;
}

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const ll maxn = ,mod = ,inf = ;

struct node
{
    ll x,y,x2,id;
}e[maxn];

ll n;
ll ans1[maxn],ans2[maxn],b[maxn],sum[maxn << ],L[maxn << ],R[maxn << ],tag[maxn << ],ans,tot;

bool cmp(node a,node b)
{
    return a.y < b.y;
}

bool cmp2(node a,node b)
{
    return a.x < b.x;
}

void pushup(ll o)
{
    sum[o] = sum[o * ] + sum[o *  + ];
    sum[o] %= mod;
}

void build(ll o,ll l,ll r)
{
    L[o] = l,R[o] = r;
    sum[o] = tag[o] = ;
    if (l == r)
        return;
    ll mid = (l + r) >> ;
    build(o * ,l,mid);
    build(o *  + ,mid + ,r);
    pushup(o);
}

void pushdown(ll o)
{
    if (tag[o])
    {
        tag[o * ] += tag[o];
        tag[o * ] %= mod;
        tag[o *  + ] += tag[o];
        tag[o *  + ] %= mod;
        sum[o * ] += tag[o] * (R[o * ] - L[o * ] + ) % mod;
        sum[o *  + ] += tag[o] * (R[o *  + ] - L[o *  + ] + ) % mod;
        tag[o] = ;
    }
}

void update(ll o,ll l,ll r,ll x,ll y,ll v)
{
    if (x > y)
        return;
    if (x <= l && r <= y)
    {
        sum[o] += (r - l + ) * 1LL * v % mod;
        sum[o] %= mod;
        tag[o] += v;
        tag[o] %= mod;
        return;
    }
    pushdown(o);
    ll mid = (l + r) >> ;
    if (x <= mid)
        update(o * ,l,mid,x,y,v);
    if (y > mid)
        update(o *  + ,mid + ,r,x,y,v);
    pushup(o);
}

void update2(ll o,ll l,ll r,ll pos,ll v)
{
    if (l == r)
    {
        sum[o] = v;
        return;
    }
    pushdown(o);
    ll mid = (l + r) >> ;
    if (pos <= mid)
        update2(o * ,l,mid,pos,v);
    else
        update2(o *  + ,mid + ,r,pos,v);
    pushup(o);
}

ll query(ll o,ll l,ll r,ll x,ll y)
{
    if (x > y)
        return ;
    if (x <= l && r <= y)
        return sum[o];
    pushdown(o);
    ll res = ;
    ll mid = (l + r) >> ;
    if (x <= mid)
        res += query(o * ,l,mid,x,y);
    res %= mod;
    if (y > mid)
        res += query(o *  + ,mid + ,r,x,y);
    res %= mod;
    return res;
}

void solve1()
{
    build(,,n);
    for (ll i = ; i <= n; i++)
    {
        ll j = i;
        while (j < n && e[i].y == e[j + ].y)
            j++;
        for (ll k = i; k <= j; k++)
            update(,,n,e[k].x2,n,-);
        for (ll k = i; k <= j; k++)
            ans1[e[k].id] = query(,,n,,e[k].x - );
        for (ll k = i; k <= j; k++)
            update2(,,n,e[k].id,e[k].x - );
        i = j;
    }
}

void solve2()
{
    build(,,n);
    for (ll i = ; i <= n; i++)
    {
        ll j = i;
        while (j < n && e[i].y == e[j + ].y)
            j++;
        for (ll k = i; k <= j; k++)
            update(,,n,,e[k].x - ,-);
        for (ll k = i; k <= j; k++)
            ans2[e[k].id] = query(,,n,e[k].x2,n);
        for (ll k = i; k <= j; k++)
            update2(,,n,e[k].id,n - e[k].x2 + );
        i = j;
    }
}

int main()
{
    scanf("%d",&n);
    for (ll i = ; i <= n; i++)
    {
        scanf("%lld%lld",&e[i].x,&e[i].y);
        b[++tot] = e[i].x;
    }
    b[++tot] = inf;
    sort(b + ,b +  + tot);
    sort(e + ,e +  + n,cmp2);
    for (ll i = ; i <= n; i++)
    {
        e[i].x2 = upper_bound(b + ,b +  + tot,e[i].x) - b;
        e[i].x = lower_bound(b + ,b +  + tot,e[i].x) - b;
        e[i].id = i;
    }
    sort(e + ,e +  + n,cmp);
    solve1();
    sort(e + ,e +  + n,cmp);
    solve2();
    for (ll i = ; i <= n; i++)
    {
        ans += ans1[i] * ans2[i] % mod;
        ans %= mod;
    }

    printf("%lld\n",ans);

    return ;
}