5. Determinant
5.1 The Properties of Determinants
The determinant of the n by n identity matrix is 1 : \(det I = 1\).
The determinant changes sign when two rows are exchanged(sign reversal) : \(det P = \pm 1\) (det P = +1 for an even number of row exchange and det P = -1 for an odd number.)
The determinant is linear function of each row separately :
- 3a : multiply row i for any number t det is multiplied by t : \(\left[ \begin{matrix} ta&tb \\ c&d \end{matrix} \right] = t\left| \begin{matrix} a&b \\ c&d \end{matrix} \right|\)
- 3b: add row i of A to row i of A' then determinants add : \(\left[ \begin{matrix} a+a'&b+b' \\ c&d \end{matrix} \right] = \left| \begin{matrix} a&b \\ c&d \end{matrix} \right| + \left| \begin{matrix} a'&b' \\ c&d \end{matrix} \right|\)
From rules 1-3 we will reach rules 4-10.
If two rows of A are equal, the det A = 0.
Subtracting a multiple of one row from another row leaves det A unchanged. ( eliminaton steps doesn't change determinant : det A = det D, without row exchanges.)
A matrix with a row of zeros has det A = 0.
If A is triangular then \(det A = a_{11}a_{22}...a_{nn}\)=product of diagnonal entries.
If A is singular then det A = 0. If A is invertible then \(det A \neq 0\).
The determinant of AB is det A times det B : \(|AB| = |A||B|\) .
The transpose \(A^T\) has the same determinant as A: \(det A^T = det A\).
- A zero column will make the det A = 0.
- Two equal columns will make the det A = 0.
- If a column is multiplied by t, so is the determinant.
5.2 Three Formula for Determinant
The Pivot Formula
When elimination leads to \(A=LU\), the pivots \(d_1,d_2,...,d_n\) are on the diagonal of the upper triangular U.
No row exchanges: \(det A = (det L)(det U)=(1)(d_1d_2...d_n)\)
Row exchanges: \((detP)(detA)= (detL)(detU)\) gives \(detA = \pm(d_1d_2...d_n)\) , odd leads to minus(-), even leads to plus(+)
The Big Formula
The big formula has n! terms.
\]
example:
\left| \begin{matrix} a_{11}&&\\ &a_{22}& \\ &&a_{33} \\\end{matrix} \right| +
\left| \begin{matrix} &a_{12}&\\ &&a_{23} \\ a_{31}&& \\\end{matrix} \right| +
\left| \begin{matrix} &&a_{13}\\ a_{21}&& \\ &a_{32}& \\\end{matrix} \right| +\\
\quad \quad \quad \quad \quad \quad \quad \quad
\left| \begin{matrix} a_{11}&&\\ &&a_{23} \\ &a_{32}& \\\end{matrix} \right| +
\left| \begin{matrix} &a_{12}&\\ a_{21}&& \\ &&a_{33} \\\end{matrix} \right| +
\left| \begin{matrix} &&a_{13}\\ &a_{22}& \\ a_{31}&& \\\end{matrix} \right| + \\
\Downarrow \\
det A = a_{11}a_{22}a_{33}\left| \begin{matrix} 1&&\\ &1& \\ &&1\\\end{matrix} \right| + a_{12}a_{23}a_{31}\left| \begin{matrix} &1&\\ &&1 \\ 1&&\\\end{matrix} \right| +
a_{13}a_{21}a_{32}\left| \begin{matrix} &&1\\ 1&& \\ &1&\\\end{matrix} \right| + \\
\quad \quad \quad
a_{11}a_{23}a_{32}\left| \begin{matrix} 1&&\\ &&1 \\ &1&\\\end{matrix} \right| +
a_{12}a_{21}a_{33}\left| \begin{matrix} &1&\\ 1&& \\ &&1\\\end{matrix} \right| +
a_{13}a_{22}a_{31}\left| \begin{matrix} &&1\\ &1& \\ 1&&\\\end{matrix} \right| \\
\quad \quad \quad
=a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} +
a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32} -
a_{12}a_{21}a_{33} -
a_{13}a_{22}a_{31}
\]
The Cofactors Formula
The determinant is the dot product of any row i of A with its cofactors using other rows:
\]
Each cofactor \(C_{ij}\) (order n-1, without row i and column j) includes its correct sign:
\]
example:
\left| \begin{matrix} a_{11}&&\\ &a_{22}&a_{23} \\ &a_{32}&a_{33} \\\end{matrix} \right| +
\left| \begin{matrix} &a_{12}&\\ a_{21}&&a_{23} \\ a_{31}&&a_{33} \\\end{matrix} \right| +
\left| \begin{matrix} &&a_{13}\\ a_{21}&a_{22}& \\ a_{31}&a_{32}& \\\end{matrix} \right|
\]
C_{12} = -(a_{21}a_{33}-a_{23}a_{31}) \\
C_{13} = a_{21}a_{32}-a_{22}a_{31}
\]
5.3 Inverse\ Cramer's Rule\ Volumn of box
Formula for \(A^{-1}\)
The i, j entry of \(A^{-1}\) is the cofactor \(C_{ji}\) divided by det A:
A^{-1} = \frac {C^T}{detA}
\]
proof :
\Uparrow \\
AC^T = (detA)I \\
\Uparrow \\
\left[ \begin{matrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \\\end{matrix} \right]
\left[ \begin{matrix} C_{11}&C_{21}&C_{31}\\ C_{12}&C_{22}&C_{32} \\ C_{13}&C_{23}&C_{33} \\\end{matrix} \right] =
\left[ \begin{matrix} detA&0&0\\ 0&detA&0 \\ 0&0&detA \\\end{matrix} \right]
\]
Cramer's Rule
If det A is not zero, Ax=b is solved by determinants:
\]
The matrix \(B_j\) has the jth column of A replaced by the vector b.
example:
det B_1 = \left| \begin{matrix} 1&a_{12}&a_{13}\\ 0&a_{22}&a_{23} \\ 0&a_{32}&a_{33} \\\end{matrix} \right| \\
det B_2 =\left| \begin{matrix} a_{11}&1&a_{13}\\ a_{21}&0&a_{23} \\ a_{31}&0&a_{33} \\\end{matrix} \right| \\
det B_3 =\left| \begin{matrix} a_{11}&a_{12}&1\\ a_{21}&a_{22}&0\\ a_{31}&a_{32}&0 \\\end{matrix} \right|
\]
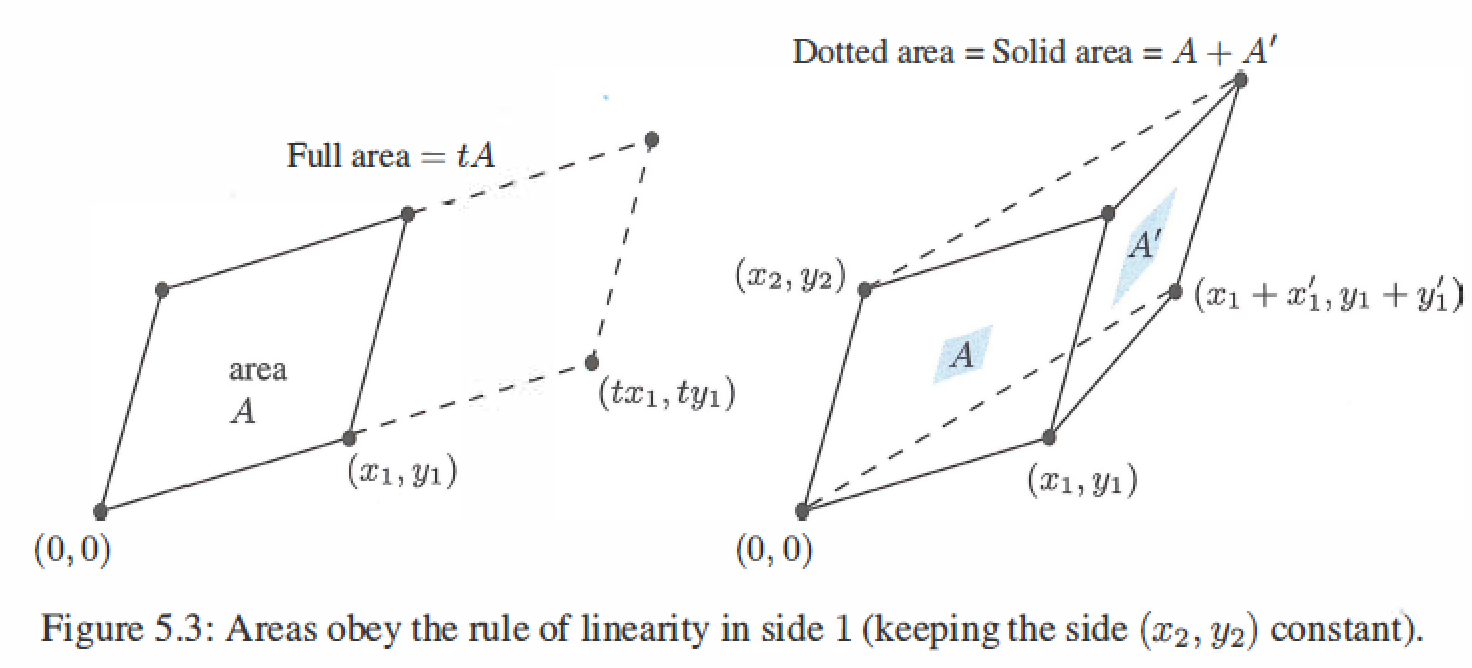
Volumn of box
The volume equals the absolute value of det A.
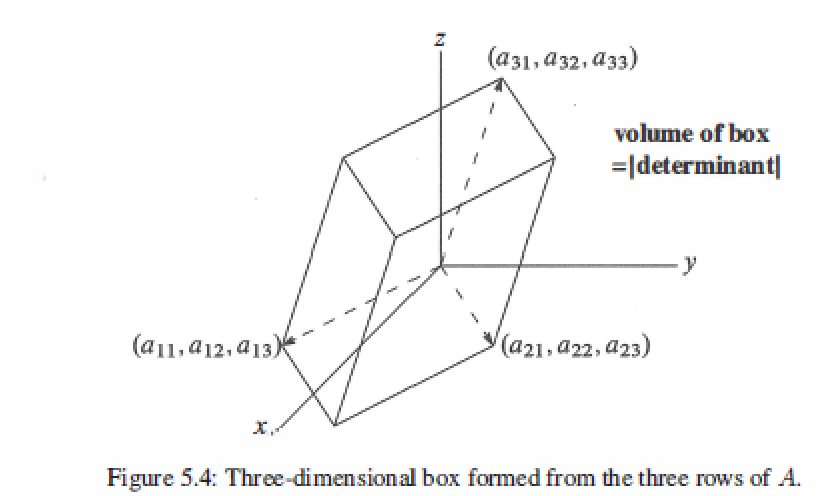
Area of Parallelogram and Triangle
Determinants are the best way to find area.
Area of Parallelogram : \(Area = Determinant\)
Area of Triangle: \(Area = Determinant / 2\)
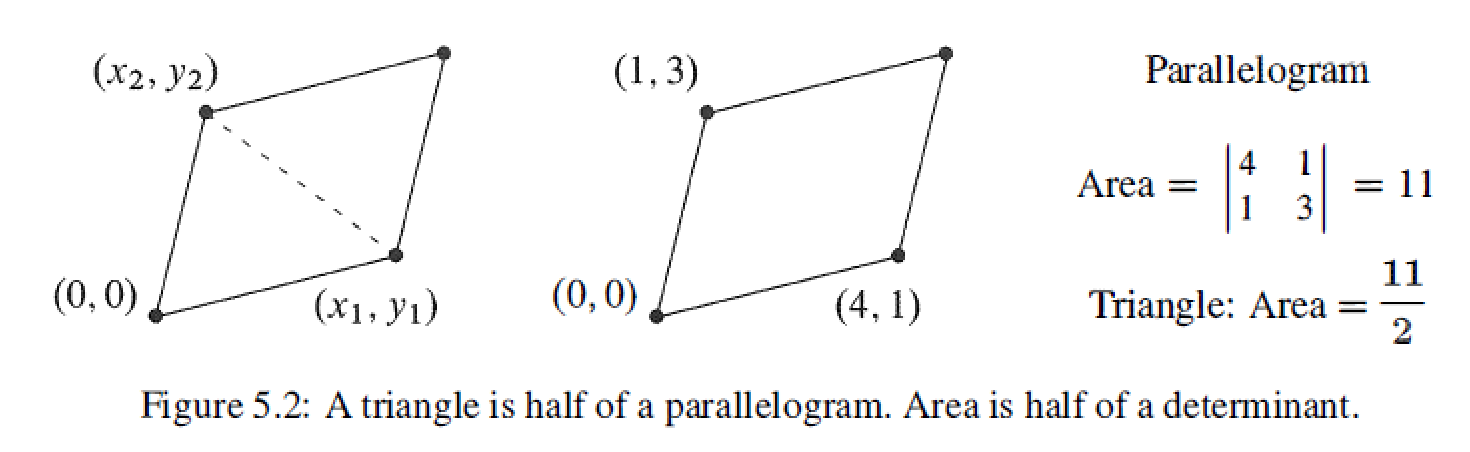
When an edge is stretched by a factor t, the volume is multiplied by t. (Rule 3a)
When edge 1 is added to edge 1', the volume is the sum of the two original volumes.(Rule 3b)
5.4 Cross Product
The cross product of \(u=(u_1,u_2,u_3)\) and \(v=(v_1,v_2,v_3)\) is a vector.
\]
The cross product is a vector with length \(||u|| \ \ ||v|| \ \ |sin\theta|\). Its direction is perpendicular to u and v.It points "up" or "down" by the right hand rule.
\]
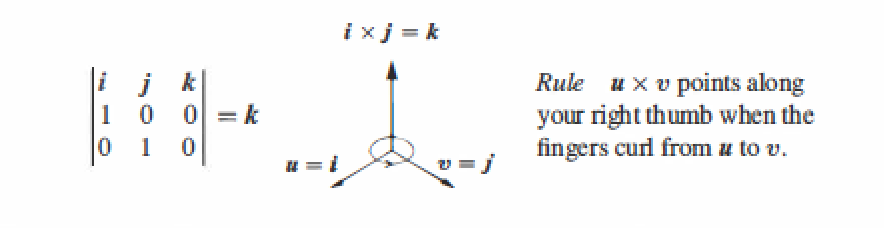
5. Determinant的更多相关文章
- bzoj 2107: Spoj2832 Find The Determinant III 辗转相除法
2107: Spoj2832 Find The Determinant III Time Limit: 1 Sec Memory Limit: 259 MBSubmit: 154 Solved: ...
- SPOJ - DETER3:Find The Determinant III (求解行列式)
Find The Determinant III 题目链接:https://vjudge.net/problem/SPOJ-DETER3 Description: Given a NxN matrix ...
- SPOJ - Find The Determinant III 计算矩阵的行列式答案 + 辗转相除法思想
SPOJ -Find The Determinant III 参考:https://blog.csdn.net/zhoufenqin/article/details/7779707 参考中还有几个关于 ...
- XTU 1260 - Determinant - [2017湘潭邀请赛A题(江苏省赛)][高斯消元法][快速幂和逆元]
是2017江苏省赛的第一题,当时在场上没做出来(废话,那个时候又不懂高斯消元怎么写……而且数论也学得一塌糊涂,现在回来补了) 省赛结束之后,题解pdf就出来了,一看题解,嗯……加一行再求逆矩阵从而得到 ...
- 2017湘潭赛 A题 Determinant (高斯消元取模)
链接 http://202.197.224.59/OnlineJudge2/index.php/Problem/read/id/1260 今年湘潭的A题 题意不难 大意是把n*(n+1)矩阵去掉某一列 ...
- Linear Algebra - Determinant(几何意义)
二阶行列式的几何意义 二阶行列式 \(D = \begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = a_1b_2 - a_2b_1\) 的几何意 ...
- Linear Algebra - Determinant(基础)
1. 行列式的定义 一阶行列式: \[ \begin{vmatrix} a_1 \end{vmatrix} = a_1 \] 二阶行列式: \[ \begin{vmatrix} a_{11} & ...
- The Evaluation of Determinant(求行列式mod一个数的值)
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #i ...
- 行列式(determinant)的物理意义及性质
1. 物理(几何)意义 detA=output areainput area 首选,矩阵代表的是线性变换(linear transformation).上式说明一个矩阵的行列式(detA)几何意义上, ...
- SP1772 Find The Determinant II
题意 \(T\) 组数据,每组给定两个整数 \(n,k\),求 \(\det A\),其中 \(A\) 为一个 \(n\times n\) 的矩阵且 \(A_{i,j}=\gcd(i,j)^k\),对 ...
随机推荐
- 符合ISO26262标准的建模规范检查模型静态分析静态测试工具
Model Examiner - 功能安全解决方案(以下简称MXAM)测试套件是您进行全面静态模型分析的首选工具.MXAM提供了一种简单的方法来检查建模规范.分析模型结构和评估模型指标,所有这些功能都 ...
- 05、secs协议常见问题分析以及如何建立通信
1.建立通信 在主机和设备之间发送SECS-II消息之前,必须首先"建立"通信.这是通过S1F13(建立通信请求)消息来完成的.这应该是在初始启动后或在长时间不通信之后发送的第一个 ...
- 【Azure Redis】Redis-CLI连接Redis 6380端口始终遇见 I/O Error
问题描述 使用Redis-cli连接Redis服务,因为工具无法直接支持TLS 6380端口连接,所以需要使用 stunnel 配置TLS/SSL服务.根据文章(Linux VM使用6380端口(SS ...
- 新零售SaaS架构:订单履约系统的概念模型设计
订单履约系统的概念模型 订单:客户提交购物请求后,生成的买卖合同,通常包含客户信息.下单日期.所购买的商品或服务明细.价格.数量.收货地址以及支付方式等详细信息. 子订单:为了更高效地进行履约,大订单 ...
- 青少年CTF-Crypto(新手版本2.0,无factor1)
凯撒大帝的征讨之路 题目: lnixoa{1x2azz7w8axyva7y1z2320vxy6v97v9a} 知识点:凯撒加密 我的题解: import base64 #shift得出移位多少,移位后 ...
- forward配置
Adb connect 127.0.0.1:62001 adb forward tcp:27042 tcp:27042 #设置端口转发 adb forward tcp:27043 tcp:27 ...
- nginx rewrite 语法
nginx rewrite 语法 一 定义 Rewrite主要实现url地址重写, 以及地址重定向,就是将用户请求web服 务器的地址重新定向到其他URL的过程. 二 语法格式 reweite fia ...
- 基于六轴传感器MPU6050的物体移动监测报警系统
一 系统简介 1.简介 MPU-60x0 是全球首例 9 轴运动处理传感器.它集成了 3 轴MEMS陀螺仪,3 轴MEMS加速度计,以及一个可扩展的数字运动处理器 DMP(Digital Motion ...
- python 判断bytes是否相等的几种方法
一 前言: python判断bytes是否相等,一般要用到这几种方法:is,==,operator.下面做几个例子让大家看一下. 二 正文: 1 相等方法: test1=b'0xab' test2=b ...
- Java使用Steam流对数组进行排序
原文地址:Java使用Steam流对数组进行排序 - Stars-One的杂货小窝 简单记下笔记,不是啥难的东西 sorted()方法里传了一个比较器的接口 File file = new File( ...
