骨牌铺方格 SDUT
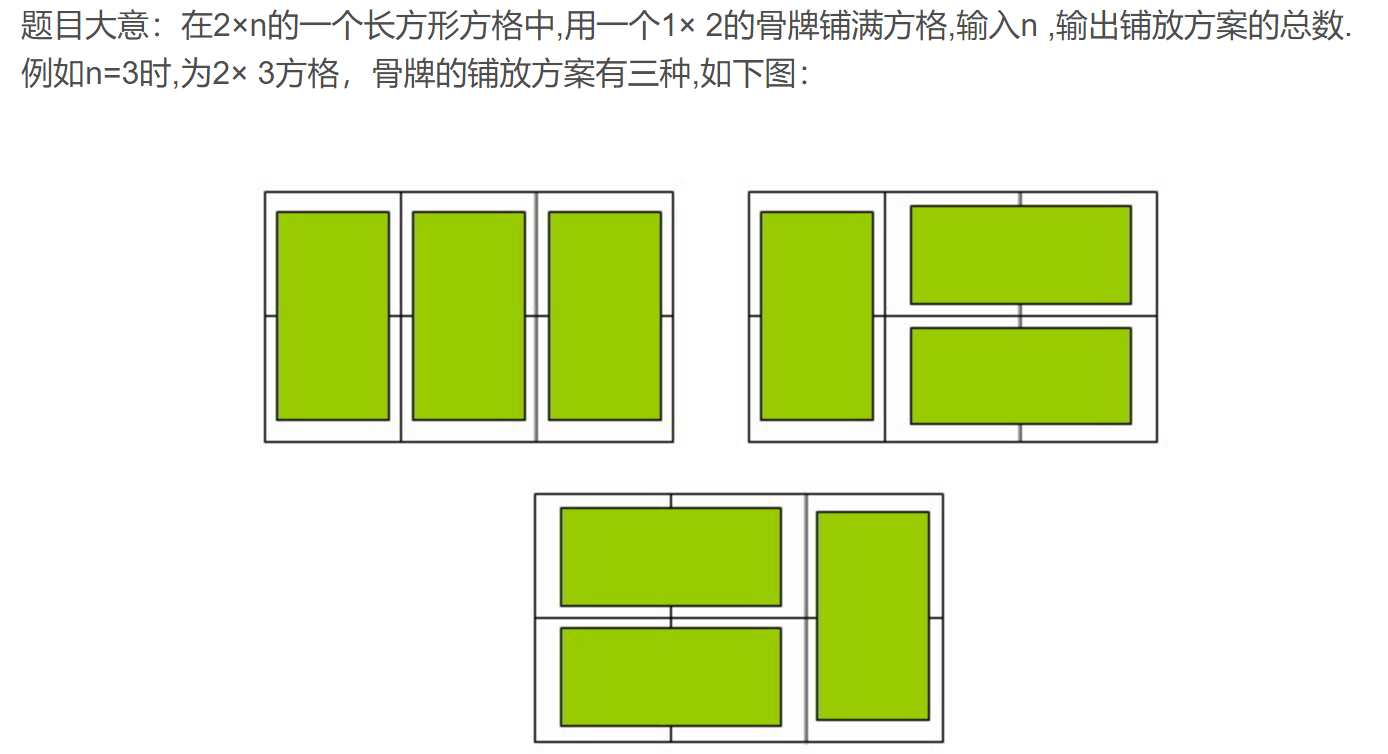
状态转移方程:dp[i] = dp[i - 1] + dp[i - 2]。
当前行,可能是由上一行转移过来的,那么当前行就只能横着铺,所以方案数是dp[i - 1]。
当前行,可能是由i-2行转移过来的, 那么就只有竖着铺俩这种方案(横着铺俩这种方案会与横着铺重复),所以是dp[i - 2]。
仔细思考,为什么不会有+1,或者+2这种情况的产生。
骨牌铺方格 SDUT的更多相关文章
- 骨牌铺方格[HDU2046]
骨牌铺方格 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submi ...
- HD2046骨牌铺方格
骨牌铺方格 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submiss ...
- hdoj 2046 骨牌铺方格
骨牌铺方格 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submi ...
- hdoj 2046 骨牌铺方格 【DP】+【斐波那契】
dp果然不是好学的... 第n个,即2*n时,可由第n-1个的竖直排列再加一个,和第n-2个中横着排两个 所以f(n) = 1×f(n-1) + 1×f(n-2): 骨牌铺方格 Time Limit: ...
- hdu_2046_骨牌铺方格_201311251403
骨牌铺方格 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Subm ...
- S - 骨牌铺方格(第二季水)
Description 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格,骨牌的铺放方案有三种, ...
- Hdoj 2046.骨牌铺方格 题解
Problem Description 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图: Inpu ...
- 1283: 骨牌铺方格(zzuli)
Problem Description 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图: Input ...
- hdu 2046 骨牌铺方格
#include<stdio.h> int main(void) { long long i,n,narr[55]; narr[1]=1;narr[2]=2;narr[3]=3; for( ...
- HDU-2046 骨牌铺方格【递推】
http://acm.hdu.edu.cn/showproblem.php?pid=2046 和前面的一样,a[i] = a[i-1] + a[i-2] #include<iostream> ...
随机推荐
- 使用Grafana 监控 minio 的部分改进
使用Grafana 监控 minio 的部分改进 部署minio开启监控metrics的脚本 mkdir -p /data/minio/data cat << EOF > /etc/ ...
- [转帖]TiDB 5.1 Write Stalls 应急文档
https://tidb.net/blog/ac7174dd#4.%E5%88%A4%E6%96%AD%E6%98%AF%E5%90%A6%E5%87%BA%E7%8E%B0%E4%BA%86%20w ...
- 【转帖】ethool工具之TSO、UFO、GSO、LRO、GRO和RSS介绍
ethtool -k < 网络接口>, ethtool --show-offload < 网络接口>, 或者可以看到很多网络接口的offload特性,例如: $ sudo et ...
- 【转帖】Linux性能优化(十三)——CPU性能测试
一.CPU上下文切换测试场景 使用sysbench模拟多线程调度: sysbench --threads=10 --time=300 threads run 使用vmstat查看CPU上下文切换: c ...
- [转帖]一本正经的八卦一下CPU的自主可控 之二
https://zhuanlan.zhihu.com/p/62399200 一本正经的八卦一下CPU的自主可控 之二 上回书说到CPU自主可控第一个层面的指令集问题.这回聊一聊接下来的设计问题. 第二 ...
- IPMI的简单使用
背景 公司一台十一年前的服务器砸到我手中,要重装CentOS7的操作系统. 本着不想进机房, 不想格式化U盘的想法, 想用BMC进行安装系统. 遇到的第一个问题是不知道密码. 询问之前的机器持有人,也 ...
- 容器方式运行Mysql8.0.26的方法
容器化运行Mysql8.0.26测试环境的方法 1. 前言 之前为了好处理,都是二进制包的方式安装mysql,但是有时候需要下载和安装也比较费时费力, 今天中午在弄Oracle RAC时想着以后能够容 ...
- [译]深入了解现代web浏览器(二)
本文是根据Mariko Kosaka在谷歌开发者网站上的系列文章https://developer.chrome.com/blog/inside-browser-part2/ 翻译而来,共有四篇,该篇 ...
- CCPC Finals 2021 H Harie Programming Contest (网络流&支配树的妙用)
Link 题意: 给一个二分图,求有多少种方案删去恰好两个点,使得最大匹配数不变.\(n,m\le 2\times 10^5\). 二话不说先跑一遍 Dinic 网络流,设残量网络形成的图为 \(G\ ...
- 【解决了一个小问题】在某个linux基础镜像中安装python特定的版本
作者:张富春(ahfuzhang),转载时请注明作者和引用链接,谢谢! cnblogs博客 zhihu Github 公众号:一本正经的瞎扯 在某个基础镜像中,安装了python3.6.但是一个测试需 ...
