Codeforces Round #FF 446 C. DZY Loves Fibonacci Numbers

參考：http://www.cnblogs.com/chanme/p/3843859.html

然后我看到在别人的AC的方法里还有这么一种神方法，他预先设定了一个阈值K,当当前的更新操作数j<K的时候，它就用一个类似于树状数组段更的方法，用一个 d数组去存内容，譬如它要在区间 [3,6]上加一段fibonacci

原来：

id 0 1 2 3 4 5 6 7 8 9 10

d  0 0 0 0 0 0 0 0 0 0 0

更新:

id 0 1 2 3 4 5 6  7  8  9 10

d  0 0 0 1 0 0 0 -5  -3 0 0

我们能够发现，当利用 d[i]=d[i]+d[i-1]+d[i-2] i由小到大更新后就会得到

id 0 1 2 3 4 5 6  7  8  9 10

d  0 0 0 1 1 2 3  0  0  0  0

所以对于[L,R]上加一段操作，我们能够d[L]+=1; d[R+1]-=f[R-L+2],d[R+2]=f[R-L+1];

所以假如我更新了m次，我每次更新的复杂度是O(1),我把全部数求出来一次的复杂度是O(n)

然后他的算法是这种，j<K的时候更新的时候依照上述方法更新，询问的话则是将询问区间和更新的区间求交，把交的和加上去。

当j==K的时候，利用d还原出新的a，把当前的区间清0.

C. DZY Loves Fibonacci Numbers

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In mathematical terms, the sequence Fn of
Fibonacci numbers is defined by the recurrence relation

F1 = 1; F2 = 1; Fn = Fn - 1 + Fn - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an.
Moreover, there are mqueries, each query has one of the two types:

1. Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to
   each element ai,
   where l ≤ i ≤ r.
2. Format of the query "2 l r". In reply to the query you should output the value of 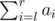 modulo 1000000009 (109 + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000).
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) —
initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

Sample test(s)

input

4 4
1 2 3 4
1 1 4
2 1 4
1 2 4
2 1 3

output

17
12

Note

After the first query, a = [2, 3, 5, 7].

For the second query, sum = 2 + 3 + 5 + 7 = 17.

After the third query, a = [2, 4, 6, 9].

For the fourth query, sum = 2 + 4 + 6 = 12.

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int maxn=330000;
const long long int mod=1000000009LL;
typedef long long int LL;

int n,m,k;
LL a[maxn],sum[maxn],fib[maxn],gib[maxn];
LL d[maxn]; int L[1100],R[1100];

void init()
{
    fib[1]=1LL,fib[2]=1LL;
    gib[1]=1LL,gib[2]=2LL;
    for(int i=3;i<=n+50;i++)
    {
        fib[i]=(fib[i-1]+fib[i-2])%mod;
        gib[i]=(gib[i-1]+fib[i])%mod;
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%I64d",a+i);
        sum[i]=sum[i-1]+a[i];
    }
    init();
    while(m--)
    {
        int c,l,r;
        scanf("%d%d%d",&c,&l,&r);
        if(c==1)
        {
            L[k]=l,R[k]=r; k++;
            d[l]=(d[l]+1LL)%mod;
            d[r+1]=(d[r+1]-fib[r-l+2]+mod)%mod;
            d[r+2]=(d[r+2]-fib[r-l+1]+mod)%mod;
            if(k>=1000)
            {
                for(int i=1;i<=n;i++)
                {
                    if(i>=2)
                        d[i]=((d[i]+d[i-1])%mod+d[i-2])%mod;
                    a[i]=(a[i]+d[i])%mod;
                    sum[i]=sum[i-1]+a[i];
                }
                memset(d,0,sizeof(d));  k=0;
            }
        }
        else if(c==2)
        {
            LL ret=0;
            for(int i=0;i<k;i++)
            {
                int _left=max(l,L[i]);
                int _right=min(r,R[i]);
                if(_left>_right) continue;
                int s=_left-L[i]+1,e=_right-L[i]+1;
                ret=((ret+gib[e])%mod-gib[s-1]+mod)%mod;
            }
            ret=((ret+sum[r])%mod-sum[l-1]+mod)%mod;
            printf("%I64d\n",(ret+mod)%mod);
        }
    }
    return 0;
}