直接理解转置卷积（Transposed convolution）的各种情况

　　使用GAN生成图像必不可少的层就是上采样，其中最常用的就是转置卷积（Transposed Convolution）。如果把卷积操作转换为矩阵乘法的形式，转置卷积实际上就是将其中的矩阵进行转置，从而产生逆向的效果。所谓效果仅仅在于特征图的形状，也就是说，如果卷积将特征图从形状a映射到形状b，其对应的转置卷积就是从形状b映射回形状a，而其中的值并不一一对应，是不可逆的。另外，不要把逆卷积（Deconvolution）和转置卷积混淆，逆卷积的目标在于构建输入特征图的稀疏编码（Sparse coding），并不是以上采样为目的的。但是转置卷积的确是来源于逆卷积，关于逆卷积与转置卷积的论文请看[1][2]。

　　下面直接对转置卷积的各种情况进行举例，从而全面理解转置卷积在Pytorch中的运算机制。使用Pytorch而不是TF的原因在于，TF中的padding方式只有两种，即valid与same，并不能很好地帮我们理解原理。而且TF和Pytorch插入0值的方式有些差异，虽然在模型层面，你只需关注模型输入输出的形状，隐层的微小差异可以通过训练来抵消，但是为了更好得把握模型结构，最好还是使用Pytorch。

　　对于Pytorch的nn.ConvTranspose2d()的参数，下面的讨论不考虑膨胀度dilation，默认为1；output_padding就是在最终的输出特征外面再加上几层0，所以也不讨论，默认为0；为了便于理解，bias也忽略不计，设为False；不失一般性，输入输出的channels都设为1。除了对将卷积转换成矩阵乘法的理解外，理解难点主要在于stride和padding的变化对转置卷积产生的影响，因此下面我们主要变化kernel_size、stride、padding三个参数来分析各种情况。

　　举例之前要注意，转换为矩阵的形式是由卷积的结果得到的，矩阵形式本身是不能直接获得的。要注意这个因果关系，转换为矩阵形式是为了便于理解，以及推导转置卷积。

实例分析

kernel_size = 2, stride = 1, padding = 0

　　首先是kernel_size = 2，stride=1，padding=0的情况，如下图：

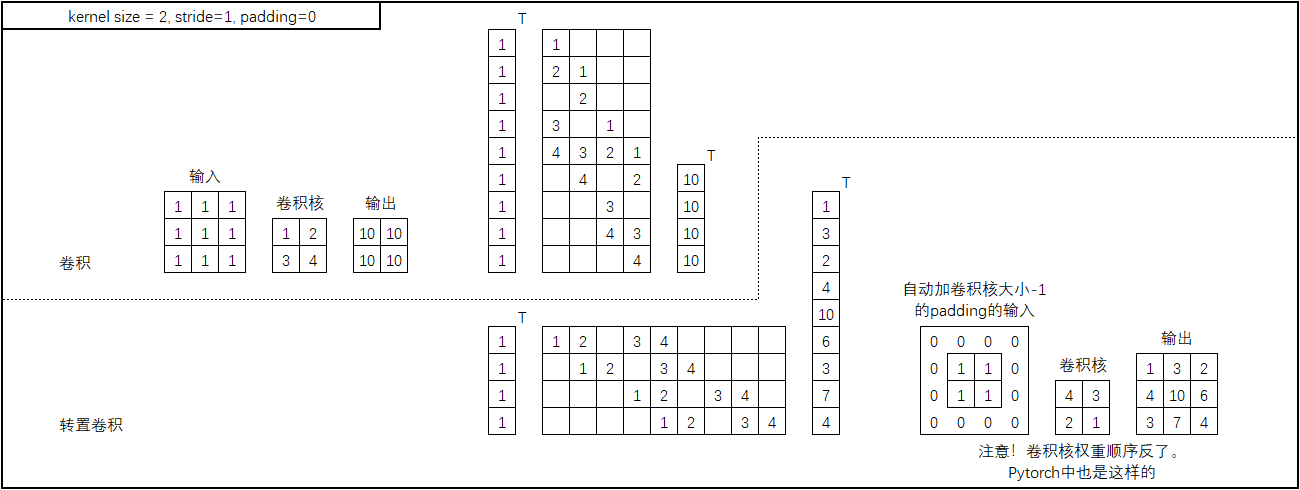
　　图中上半部分表示将卷积转换为矩阵乘法的形式。在卷积中，我们是输入一个3x3的特征图，输出2x2的特征图，矩阵乘法形式如上图上中部分所示；转置卷积就是将这个矩阵乘法反过来，如上图下中部分所示。然后将下中部分的矩阵乘法转换为卷积的形式，即可得到转置卷积的示意图如上图右下部分所示。

kernel_size = 2, stride = 1, padding = 1

　　然后是kernel_size = 2，stride=1，padding=1的情况（因为第一张图中已有，虚线与注释都不加了）：

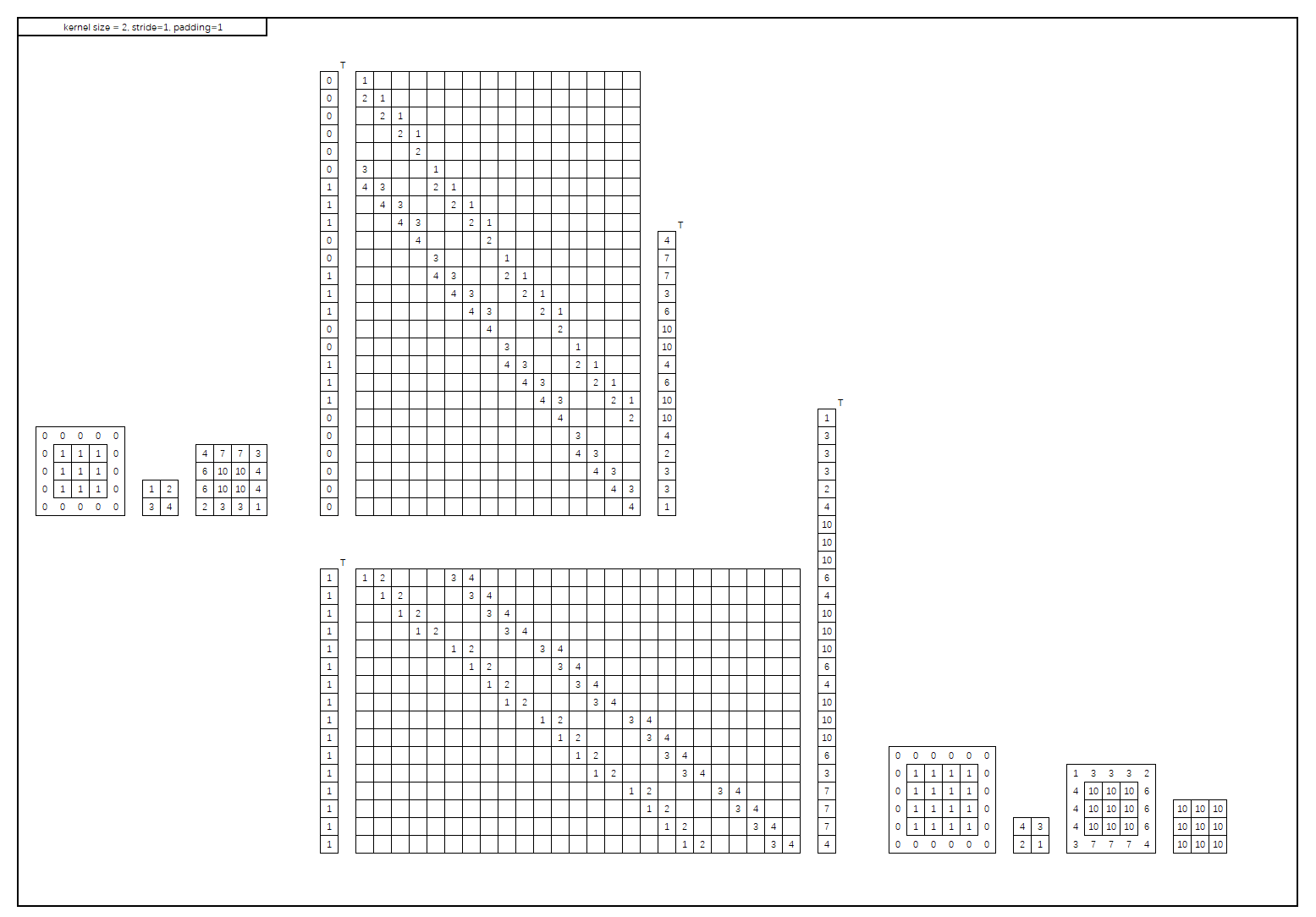
　　与上一张图的主要不同之处在于转置卷积将卷积结果的最外层去掉，这是因为padding=1，也正符合与卷积相反的操作。也就是说，padding越大，转置卷积就会去掉越多的外层，输出就会越小。

kernel_size = 3, stride = 1, padding = 1

　　为了分析转置卷积的卷积核与卷积的卷积核的区别，这次把kernel_size变为3，如下图：

　　可以看出，转置卷积的先将输入padding 2层，用于抵消卷积核带来的规模上的减小，从而将输出扩增到相对应卷积操作的输入大小。然后，我们可以发现，卷积核是输入的卷积核的逆序。也就是说，我们输入函数中的是1~9的方阵，而它实际作为卷积核的是9~1的方阵。最后，因为padding=1，这对于卷积操作是向外加一层0，而对于逆卷积，就是去掉最外面的一层，所以得到最终3x3的结果。

kernel_size = 2, stride = 2, padding = 1

　　最后，分析stride对转置卷积的影响，将stride设为2，如下图：

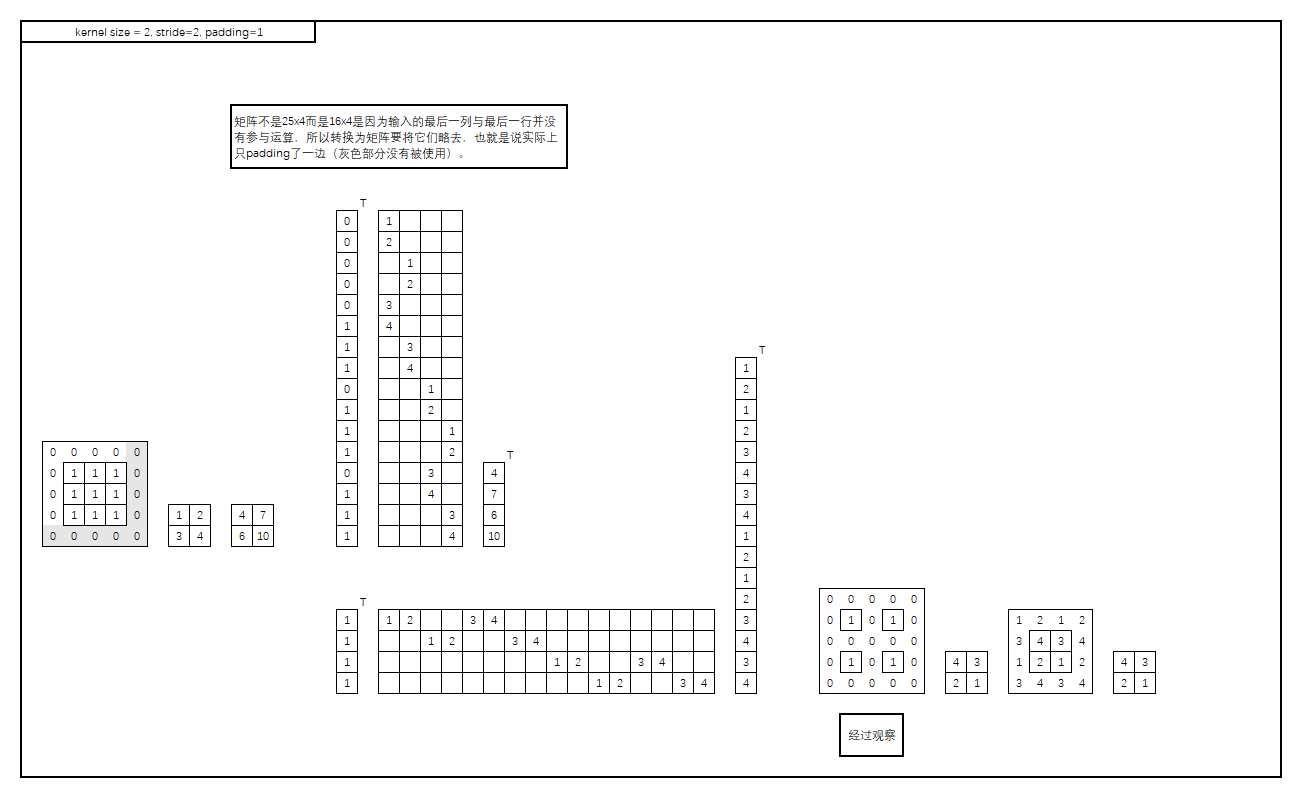
　　分析在图中都已写明。你可能会奇怪，为什么这里转置卷积最终输出与卷积的输入形状不同，这是因为卷积的padding并没有被全都用上（只计算了一边），而转置卷积最后却把两边的padding都去掉了，所以造成了卷积与转置卷积不对应的情况。

总结

　　经过对以上各种实例的分析，对于某个$kernel \,size=k,stride=s,padding=p$的转置卷积，如果输入宽高都为$n$，则输出宽高为

$\begin{aligned} m&=ns-(s-1)+2(k-1)-(k-1)-2p\\ &=(n-1)s-2p+k   \\ \end{aligned}$

　　实际上，卷积与转置卷积除了输入输出的形状上相反以外，没有别的联系，所以我们只要会计算转置卷积输出的形状即可。

　　以上图都是用excel作的，已上传至博客园文件，需要的可以下载（点击链接）。

参考文献

　　[1] Zeiler M D, Krishnan D, Taylor G W, et al. Deconvolutional networks[C]. Computer Vision and Pattern Recognition, 2010.

　　[2] Zeiler M D, Fergus R. Visualizing and Understanding Convolutional Networks[C]. European Conference on Computer Vision, 2013.