题解 洛谷P6853 station

蒟蒻语

还是蒟蒻太菜了，这场 div1 竟然一题都没做出来/kk/kk/kk

蒟蒻解

首先我们把每 5 个点分为一组。然后分组结果大概是这样子：

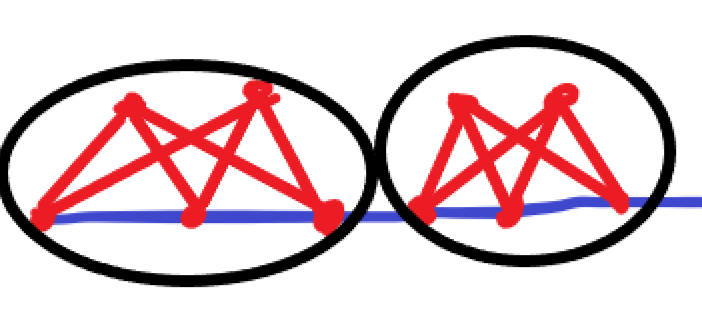
可以看到首先下面需要有一条边来让整张图有一条支撑的路径。然后每一组内都有 6 条边。

那么这样子的图是可行的。原因：

1. 对于每条线路，都至少经过两个车站，满足第一个条件。
2. 对于所有点，经过他的路径数不超过 \(3\)，满足第二个条件。
3. 对于任意两条边， 都与最下面的那条边有交点，满足第三个条件。

那么可以先将边的数量-1， 然后再按模 6 的余数分类，单独处理 (细节看代码)。

---

小蒟蒻太菜了，不会证明这为什么这样点数是最小的。

蒟蒻码

#include<bits/stdc++.h>
#define re register
#define L(i, j, k) for(re int i = j; i <= k; i++)
#define R(i, j, k) for(re int i = j; i >= k; i--)
#define db double
#define ll long long
using namespace std;
int n, m, tot;
void print(int x) { // 把每一个组内的点输出
	L(i, 1, x) {
		L(j, 1, 3) printf("2 %d %d\n", (i - 1) * 5 + 1, (i - 1) * 5 + 2 + j);
		L(j, 1, 3) printf("2 %d %d\n", (i - 1) * 5 + 2, (i - 1) * 5 + 2 + j);
	}
}
int main() {
    scanf("%d", &n), n--; // 先在最下面放一条线
    int ds = n / 6 * 5;
    if(n % 6 == 0) {
 	   	printf("%d\n", ds);
		printf("%d ", ds / 5 * 3);
		L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i) // 输出这一个组内元素
		puts("");
 	   	print(ds / 5);
	}
	else if(n % 6 == 1) {
		ds -= 5;  // 特别注意一下，为了让剩下的那条边有依靠，这里是把一个组再拆开来qwq
 	   	printf("%d\n", ds + 7);
		printf("%d ", ds / 5 * 3 + 4);
		L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
		printf("%d %d %d %d\n", ds + 1, ds + 2, ds + 3, ds + 4);
	   	print(ds / 5);
	   	printf("2 %d %d\n", ds + 5, ds + 1); // 处理不属于那一组一组的那些边
 	   	printf("2 %d %d\n", ds + 5, ds + 2);
 	   	printf("2 %d %d\n", ds + 5, ds + 3);
 	   	printf("2 %d %d\n", ds + 6, ds + 2);
 	   	printf("2 %d %d\n", ds + 6, ds + 3);
 	   	printf("2 %d %d\n", ds + 7, ds + 1);
 	   	printf("2 %d %d\n", ds + 7, ds + 4);
	} // 后面的分类讨论和上面的几乎一样
	else if(n % 6 == 2) {
		printf("%d\n", ds + 3);
		printf("%d ", ds / 5 * 3 + 2);
		L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
		printf("%d %d\n", ds + 1, ds + 2);
	   	print(ds / 5);
	   	printf("2 %d %d\n", ds + 3, ds + 1);
 	   	printf("2 %d %d\n", ds + 3, ds + 2);
	}
	else if(n % 6 == 3) {
 	   	printf("%d\n", ds + 4);
		printf("%d ", ds / 5 * 3 + 3);
		L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
		printf("%d %d %d\n", ds + 1, ds + 2, ds + 3);
	   	print(ds / 5);
 	   	printf("2 %d %d\n", ds + 4, ds + 1);
 	   	printf("2 %d %d\n", ds + 4, ds + 2);
 	   	printf("2 %d %d\n", ds + 4, ds + 3);
	}
	else if(n % 6 == 4) {
	   	printf("%d\n", ds + 4);
		printf("%d ", ds / 5 * 3 + 2);
		L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
		printf("%d %d\n", ds + 1, ds + 2);
	   	print(ds / 5);
	   	printf("2 %d %d\n", ds + 3, ds + 1);
	   	printf("2 %d %d\n", ds + 3, ds + 2);
	   	printf("2 %d %d\n", ds + 4, ds + 1);
	   	printf("2 %d %d\n", ds + 4, ds + 2);
	}
	else if(n % 6 == 5) {
 	   	printf("%d\n", ds + 5);
		printf("%d ", ds / 5 * 3 + 3);
		L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
		printf("%d %d %d\n", ds + 1, ds + 2, ds + 3);
 	   	print(ds / 5);
 	   	printf("2 %d %d\n", ds + 4, ds + 1);
 	   	printf("2 %d %d\n", ds + 4, ds + 2);
 	   	printf("2 %d %d\n", ds + 5, ds + 1);
 	   	printf("2 %d %d\n", ds + 5, ds + 2);
 	   	printf("2 %d %d\n", ds + 5, ds + 3);
	}
	return 0;
}