数据结构-kmp算法

定义 改进字符串的匹配算法

关键：通过实现一个包含了模式串的局部匹配信息的next()函数，利用匹配失败的信息，减少匹配次数。

1.BF算法 暴力匹配

给定 文本串S “BBC ABCDAB ABCDABCDABDE” 存储为 s[i]   和模式串 P “ABCDABD”   存储为p[j] 进行匹配

思路

p串与S串逐一匹配 ，不匹配则 p串右移一位，匹配下一个 。

p串不断右移 直到第四位匹配成功

不断向后匹配 直到失败

i，j回退到p串在s串的初始位置，p串右移匹配下一位。

暴力代码：

int ViolentMatch(char* s, char* p)
{
	int sLen = strlen(s);
	int pLen = strlen(p);

	int i = 0;
	int j = 0;
	while (i < sLen && j < pLen){
		if (s[i] == p[j]){  //①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++
			i++;
			j++;
		}
		else{//     ②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0
			i = i - j + 1;
			j = 0;
		}
	}
	if (j == pLen)//匹配成功，返回模式串p在文本串s中的位置，否则返回-1
		return i - j;
	else
		return -1;
}

2. kmp算法 优化匹配（利用next() 优化）

KMP算法和BF算法的“开局”是一样的，同样是把主串和模式串的首位对齐，从左到右对逐个字符进行比较。

第一轮，模式串和主串的第一个等长子串比较，发现前5个字符都是匹配的，第6个字符不匹配，是一个“坏字符”：

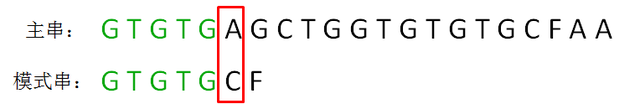
这时候，如何有效利用已匹配的串 “GTGTG” 呢？

我们可以发现，在串GTGTG”当中，后三个字符“GTG”和前三位字符“GTG”是相同的：

在下一轮的比较时，把这两个相同的片段对齐，出现匹配。 GTG 是串GTGTG 前缀后缀公共元素中最长的

第二轮，我们直接把模式串向后移动两位，让两个“GTG”对齐，继续从刚才主串的坏字符A开始进行比较：

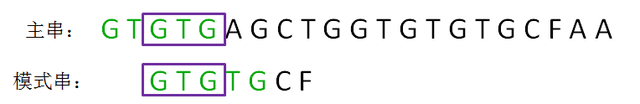
显然，主串的字符A仍然是坏字符，这时候已经匹配的串缩短成了GTG：

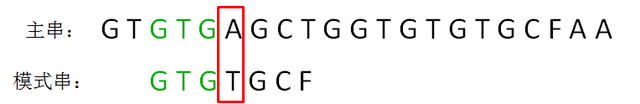
按照第一轮的思路，我们来重新确定 前缀后缀最长公共元素：

第三轮，我们再次把模式串向后移动两位，让两个“G”对齐，继续从刚才主串的坏字符A开始进行比较：

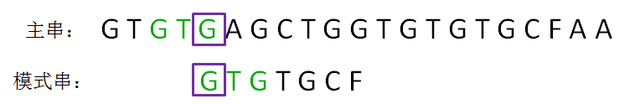
以上就是KMP算法的整体思路：在已匹配的串当中寻找到 前缀后缀最长公共元素，在下一轮直接把两者对齐，从而实现模式串的快速移动。

3.求出next()函数的方式 

①寻找前缀后缀最长公共元素长度

基本概念：

字符串abcda为例子

前缀 ： 最后一个字符以外，一个字符串的全部头部组合。 例子abcda的前缀为 a ab abc abcd

后缀 ： 第一个字符以外，一个字符串的全部尾部组合。     例子abcd的后缀为 bcda cda da  a

前缀后缀最长公共元素 ： 前缀后缀相同的元素，且长度最长的一个。例子的共同元素为a 长度为1

给定一个模式串  GTGTGCF

G无前缀后缀 公共元素长度为0

GT 前缀 G 后缀T公共元素长度为0

GTG  前缀G GT   后缀 TG G 公共元素G 长度为1

GTGT前缀 G GT GTG 后缀 TGT GT G 公共元素 GT 长度为 2

GTGTG  前缀G GT  GTG GTGT 后缀 TGTG GTG TG G 公共元素GTG 长度为3

GTGTGC  前缀G GT  GTG GTGT GTGTG   后缀 TGTGC GTGC TGC GC C  公共元素长度为0

GTGTGCF 前缀G GT  GTG GTGT GTGTG   GTGTGC 后缀 TGTGCF GTGCF TGCF GCF CF公共元素长度为0

得到串的 前缀后缀最长公共元素长度 如表

各个子串的最后一位对应该串的 最长公共元素长度

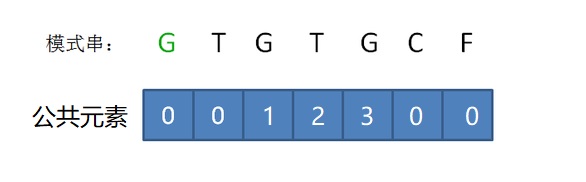
②求next数组

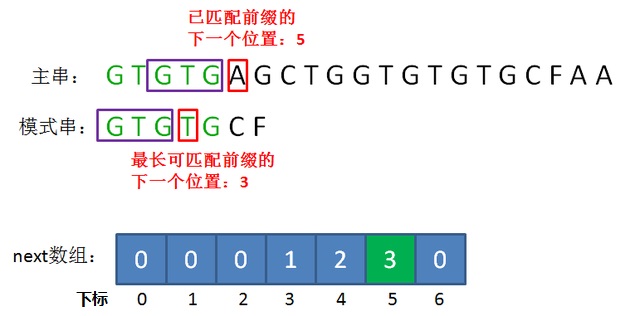
next数组 是一维整型数组，数组的下标代表了“已匹配串的长度 也是 已匹配串的下一位置 ”，

元素的值则是“  已匹配串 前缀后缀最长公共元素 的长度 也是  已匹配串 前缀后缀最长公共元素 的下一个位置”。

通过next数组即可将公共元素部分对齐

void GetNext(char* p,int next[])
{
    int pLen = strlen(p);
    next[0] = 0;
    int k = -1;
    int j = 0;
    while (j < pLen - 1)
    {
        //p[k]表示前缀，p[j]表示后缀
        if (k == -1 || p[j] == p[k])
        {
            ++k;
            ++j;
            next[j] = k;
        }
        else
        {
            k = next[k];
        }
    }
}  

代码

int KmpSearch(char* s, char* p)
{
    int i = 0;
    int j = 0;
    int sLen = strlen(s);
    int pLen = strlen(p);
    while (i < sLen && j < pLen)
    {
        //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++
        if (j == -1 || s[i] == p[j])
        {
            i++;
            j++;
        }
        else
        {
            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]
            j = next[j];
        }
    }
    if (j == pLen)
        return i - j;
    else
        return -1;
}

4 kmp对next()的进一步优化

扩展算法

1.BM算法

2 study算法