uva 11971 Polygon

https://vjudge.net/problem/UVA-11971

有一根长度为n的木条，随机选k个位置把它们切成k+1段小木条。求这些小木条能组成一个多边形的概率。

将木条看做一个圆，线上切k刀等价于圆上切k+1刀

如果能组成多边形，每一段木条的长度都要<圆周长/2

反过来，如果不能组成多边形，有且仅有一段长度>=圆周长/2

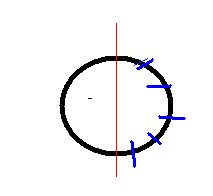
如图所示，第一刀可以随便切，接下来的每一刀都要在第一刀所在的那个半圆上

概率=（1/2）^k

每一个切点处，都可以断开成为线，共有k+1种断法

所以不能构成多边形的概率=（k+1）*（1/2）^K

答案就是用1减去它

注意：这是几何概型，可能情况无限，所以不能分析每一刀具体切在哪儿

#include<cstdio>
#include<algorithm>
using namespace std;
long long fz,fm,gcd;
long long bit[];
int main()
{
    int t,n,k;
    bit[]=;
    for(int i=;i<=;i++) bit[i]=bit[i-]*;
    scanf("%d",&t);
    for(int i=;i<=t;i++)
    {
        scanf("%d%d",&n,&k);
        fz=bit[k]-k-;
        fm=bit[k];
        gcd=__gcd(fz,fm);
        fz/=gcd; fm/=gcd;
        printf("Case #%d: %lld/%lld\n",i,fz,fm);
    }
}