动态规划-Minimum Insertion Steps to Make a String Palindrome

2020-01-05 11:52:40

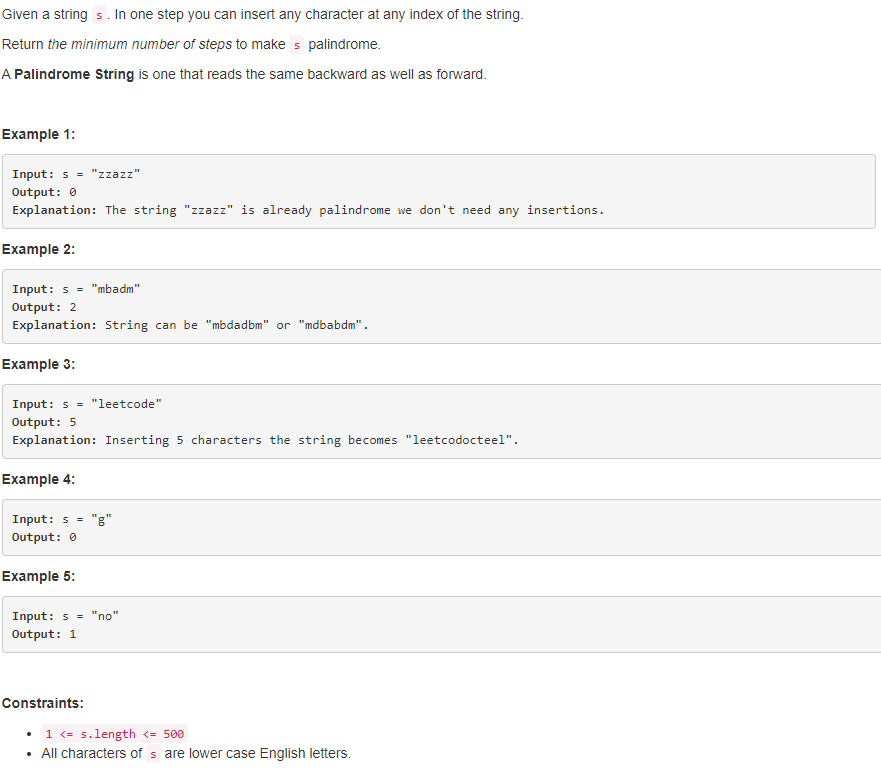
问题描述：

问题求解：

好像多次碰到类似的lcs的变种题了，都是套上了回文的壳。这里再次记录一下。

其实本质就是裸的lcs，就出结果了。

    public int minInsertions(String s) {
        StringBuffer sb = new StringBuffer(s);
        String b = sb.reverse().toString();
        return s.length() - lcs(s, b);
    }

    public int lcs(String str1, String str2) {
        int len1 = str1.length();
        int len2 = str2.length();
        int c[][] = new int[len1+1][len2+1];
        for (int i = 0; i <= len1; i++) {
            for( int j = 0; j <= len2; j++) {
                if(i == 0 || j == 0) {
                    c[i][j] = 0;
                } else if (str1.charAt(i-1) == str2.charAt(j-1)) {
                    c[i][j] = c[i-1][j-1] + 1;
                } else {
                    c[i][j] = Math.max(c[i - 1][j], c[i][j - 1]);
                }
            }
        }
        return c[len1][len2];
    }