数学--数论--HDU 1098 Ignatius's puzzle （费马小定理+打表）

Ignatius’s puzzle

Problem Description

Ignatius is poor at math,he falls across a puzzle problem,so he has no choice but to appeal to Eddy. this problem describes that:f(x)=5x^13+13*x5+ka*x,input a nonegative integer k(k<10000),to find the minimal nonegative integer a,make the arbitrary integer x ,65|f(x)if

no exists that a,then print “no”.

Input

The input contains several test cases. Each test case consists of a nonegative integer k, More details in the Sample Input.

Output

The output contains a string “no”,if you can’t find a,or you should output a line contains the a.More details in the Sample Output.

Sample Input

11 100 9999

Sample Output

22 no 43

Author

eddy

Recommend

We have carefully selected several similar problems for you: 1071 1014 1052 1097 1082

题目大意：

给定一个k，找到最小的a 使得 f(x)=5x^13+13*x5+ka*x ，f(x)%65永远等于0

打表的话就很明显的看导规律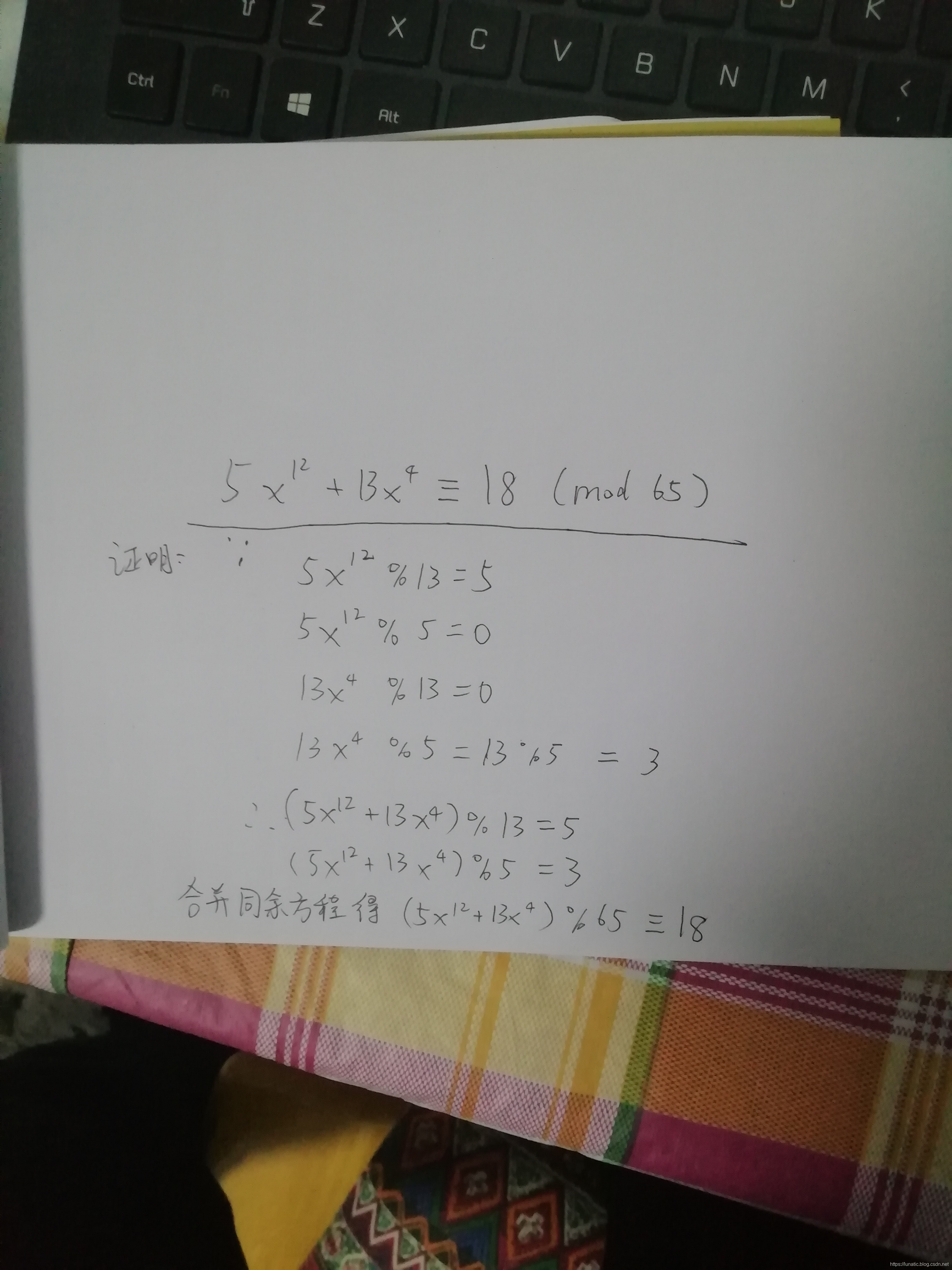

也可以用费马小定理证明

#include <iostream>
#include <cstdio>
using namespace std;
int gcd(int a, int b)
{
    if (a < b)
        return gcd(b, a);
    if (b == 0)
        return a;
    if ((a & 1) == 0 && (b & 1) == 0)
        return 2 * gcd(a >> 1, b >> 1); //a and b are even
    if ((a & 1) == 0)
        return gcd(a >> 1, b); // only a is  even
    if ((b & 1) == 0)
        return gcd(a, b >> 1);              // only b is  even
    return gcd((a + b) >> 1, (a - b) >> 1); // a and b are odd
}
int main()
{
    int k;
    while (scanf("%d", &k) != EOF)
    {
        if (18 % gcd(k, 65) == 0)
        {
            for (int a = 0;; a++)
            {
                if ((18 + k * a) % 65 == 0)
                {
                    printf("%d\n", a);
                    break;
                }
            }
        }
        else
            printf("no\n");
    }
    return 0;
}